题目内容
设
为奇函数，
为常数．
（1）求的值；
（2）证明
在区间（1，＋∞）内单调递增；
（3） 若对于区间[3,4]上的每一个
的值，不等式>
恒成立，求实数
的取值范围．
（1）
（2）证明见解析
（3）
解析:
（1）法一：由为奇函数得的定义域关于数0对称
则
故……………………………………………………3分
经检验，当时为奇函数. …………………4分
法二：由为奇函数得
即
经检验，当
时不合条件
故……………………………………………………4分
（2）由（1）得
设
为
上任意两个实数，且
，则
在区间（1，＋∞）内单调递增.…………………………10分
（3）令
，则由（2）得
在
上单调递增…………13分
……………………………………………………16分
…………………………………………………………………18分
练习册系列答案
相关题目
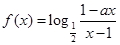为奇函数，
为常数。
在（1，＋∞）内单调递增；
的值，不等式
恒成立，求实数
的取值范围。
为奇函数，
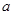为常数．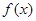
在区间（1，＋∞）内的单调性，并证明你的判断正确；
的值，不等式
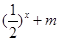恒成立，求实数
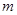的取值范围．
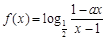为奇函数，
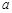为常数．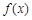
在区间（1，＋∞）的单调性，并说明理由；
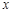值，不等式
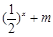恒成立，求实数
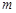的取值范围．
为奇函数，
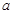为常数。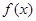
在（1，＋∞）内单调递增；
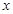的值，不等式
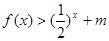恒成立，求实数
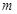的取值范围。