题目内容
已知函数 的最小正周期为
的最小正周期为 .
.
(I)求 值及
值及 的单调递增区间;
的单调递增区间;
(II)在△ 中,
中, 分别是三个内角
分别是三个内角 所对边,若
所对边,若 ,
, ,
, ,求
,求 的大小.
的大小.
 的最小正周期为
的最小正周期为 .
.(I)求
 值及
值及 的单调递增区间;
的单调递增区间;(II)在△
 中,
中, 分别是三个内角
分别是三个内角 所对边,若
所对边,若 ,
, ,
, ,求
,求 的大小.
的大小.(I) ;
; 的单调递增区间为
的单调递增区间为 ;(II)
;(II) 或
或 .
.
 ;
; 的单调递增区间为
的单调递增区间为 ;(II)
;(II) 或
或 .
.试题分析:(I)由已知首先利用降幂扩角和倍角公式:
 ,将函数
,将函数 化为一个角的三角函数,利用公式
化为一个角的三角函数,利用公式 求
求 值,利用整体思想求
值,利用整体思想求 的单调递增区间;(II)由(I)
的单调递增区间;(II)由(I) 及已知
及已知 ,得
,得 ,由此可以求得
,由此可以求得 角.再利用正弦定理,得
角.再利用正弦定理,得 ,结合已知条件
,结合已知条件 ,可求得角
,可求得角 的大小.
的大小. 试题解析:(I)
 ,
, 最小正周期为
最小正周期为 ,
, .
. 单调递增区间为
单调递增区间为 .
.(II)

 由正弦定理
由正弦定理 ,
,
 或
或 .
.
练习册系列答案
相关题目
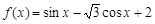 ,记函数
,记函数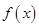 的最小正周期为
的最小正周期为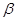 ,向量
,向量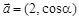 ,
,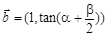 (
(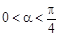 ),且
),且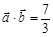 .
.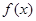 在区间
在区间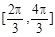 上的最值;
上的最值;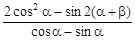 的值.
的值. 已知BC平行于x轴,AB所在直线方程为
已知BC平行于x轴,AB所在直线方程为 ,记角A,B,C所对的边分别是a,b,c.
,记角A,B,C所对的边分别是a,b,c.
 的值;
的值; 的值.
的值.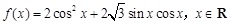 .
.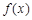 的最小正周期;
的最小正周期;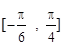 上的值域.
上的值域.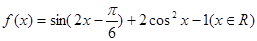
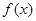 的单调递增区间;
的单调递增区间;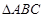 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为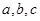 ,已知
,已知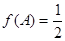 ,
,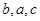 成等差数列,且
成等差数列,且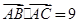 ,求边
,求边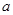 的值.
的值. .
. 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 ,求
,求 的值.
的值.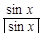 +
+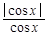 +
+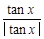 的值域是( )
的值域是( ) 的最小值和最大值分别为( )
的最小值和最大值分别为( ) 3,1
3,1
 -ax(a∈R)既有最大值又有最小值,则f(x)值域为_______.
-ax(a∈R)既有最大值又有最小值,则f(x)值域为_______.