题目内容
设{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110且a1,a2,a4成等比数列,
(1)证明a1=d;
(2)求公差d的值和数列{an}的通项公式。
(1)证明a1=d;
(2)求公差d的值和数列{an}的通项公式。
(1)证明:因 成等比数列,故
成等比数列,故 ,
,
而{an}是等差数列,有 ,
,
于是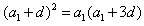 ,
,
即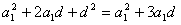 ,
,
化简得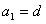 ;
;
(2)解:由条件 和
和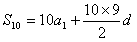 ,
,
得到 ,
,
由(1), ,
,
代入上式得55d=110,
故d=2,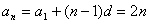
因此,数列{an}的通项公式为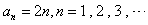 。
。

练习册系列答案
相关题目