题目内容
(本题满分14分)
已知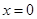 是函数
是函数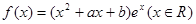 的一个极值点,且函数
的一个极值点,且函数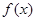 的图象在
的图象在 处的切线的斜率为2
处的切线的斜率为2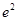 .
.
(Ⅰ)求函数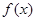 的解析式并求单调区间.(5分)
的解析式并求单调区间.(5分)
(Ⅱ)设 ,其中
,其中 ,问:对于任意的
,问:对于任意的 ,方程
,方程
 在区间
在区间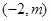 上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
(I)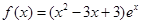 ,单调增区间是
,单调增区间是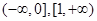 ,单调减区间是
,单调减区间是 ;
;
(Ⅱ)对于任意的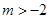 ,方程
,方程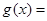
 在区间
在区间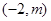 上均有实数根且当
上均有实数根且当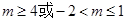 时,有唯一的实数解;当
时,有唯一的实数解;当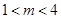 时,有两个实数解。
时,有两个实数解。
【解析】
试题分析:(Ⅰ)由x=0是函数f(x)=(x2+ax+b)ex(x∈R)的一个极值点,f′(0)=0,得到关于a,b的一个方程,函数f(x)的图象在x=2处的切线的斜率为2e2,f′(2)=2e2;得到一个关于a,b的一个方程,解方程组求出a,b即可;
(Ⅱ)把求得的f′(x)代入g(x),方程g(x)=(m-1)2在区间(-2,m)上是否存在实数根,转化为求函数g(x)在区间(-2,m)上的单调性、极值、最值问题.
解:(I)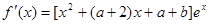 ………………1分
………………1分
由
 ……………………2分
……………………2分
又
 ,故
,故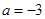 ………3分
………3分
令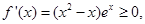 得
得 或
或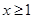
令 得
得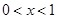 ………………4分
………………4分
故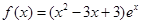 ,单调增区间是
,单调增区间是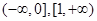 ,单调减区间是
,单调减区间是 ……5分.
……5分.
(Ⅱ)解:假设方程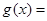
 在区间
在区间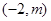 上存在实数根
上存在实数根
设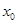 是方程
是方程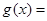
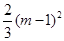 的实根,
的实根, ,………………6分
,………………6分
令 ,从而问题转化为证明方程
,从而问题转化为证明方程 =0
=0
在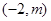 上有实根,并讨论解的个数……………………7分
上有实根,并讨论解的个数……………………7分
因为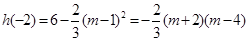 ,
,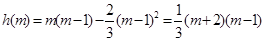 ,
,
所以 ①当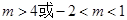 时,
时,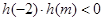 ,所以
,所以 在
在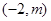 上有解,且只有一解.…………………………9分
上有解,且只有一解.…………………………9分
②当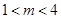 时,
时,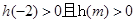 ,但由于
,但由于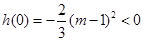 ,
,
所以 在
在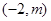 上有解,且有两解 ……………………………10分
上有解,且有两解 ……………………………10分
③当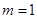 时,
时, ,所以
,所以 在
在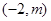 上有且只有一解;
上有且只有一解;
当 时,
时,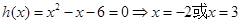 ,
,
所以 在
在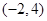 上也有且只有一解…………………………………12分
上也有且只有一解…………………………………12分
综上, 对于任意的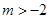 ,方程
,方程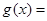
 在区间
在区间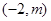 上均有实数根且当
上均有实数根且当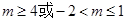 时,有唯一的实数解;当
时,有唯一的实数解;当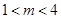 时,有两个实数解……14分
时,有两个实数解……14分
考点:本试题主要考查了函数在某点取得极值的条件和导数的几何意义,求函数f(x)的解析式体现了方程的思想;方程根的个数问题转化为求函数的最值问题,体现了转化的思想方法,再求函数最值中,又用到了分类讨论的思想;属难题
点评:解决该试题的关键是方程根的个数问题转化为求函数的最值问题,并能利用导数的几何意义求解切线方程问题。

 阅读快车系列答案
阅读快车系列答案 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).