题目内容
(14分). 设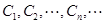 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在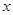 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线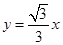 相切,对每一个正整数
相切,对每一个正整数 ,圆
,圆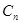 都与圆
都与圆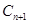 相互外切,以
相互外切,以 表示
表示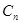 的半径,已知
的半径,已知 为递增数列.
为递增数列.
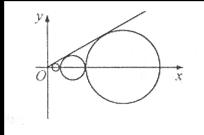
(Ⅰ)证明: 为等比数列;
为等比数列;
(Ⅱ)设 ,求数列
,求数列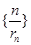 的前
的前 项和.
项和.
【答案】
(Ⅰ)略
(Ⅱ)
【解析】解:
(Ⅰ)将直线 的倾斜角记为
的倾斜角记为 ,则有
,则有 ,
, ,设
,设 的圆心为
的圆心为 ,则由题意知
,则由题意知 ,得
,得 ;同理
;同理 ,从而
,从而 ,将
,将 代入,解得
代入,解得
故 为公比q=3的等比数列
为公比q=3的等比数列
(Ⅱ)由于 ,
, ,故
,故 ,从而
,从而 ,记
,记 ,
,
则有 ①
①
 ②
②
① - ②,得

=
∴

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 、
、 ,坐标平面上点An、Bn(n∈N*)分别满足下列两个条件:
,坐标平面上点An、Bn(n∈N*)分别满足下列两个条件: 且
且 =
= 且
且 =
= .
.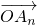 及
及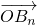 的坐标;
的坐标; 、
、 ,坐标平面上点An、Bn(n∈N*)分别满足下列两个条件:
,坐标平面上点An、Bn(n∈N*)分别满足下列两个条件: 且
且 =
= +
+ ;②
;② 且
且 =
= .
. 及
及 的坐标;
的坐标; 、
、 ,坐标平面上点An、Bn(n∈N*)分别满足下列两个条件:
,坐标平面上点An、Bn(n∈N*)分别满足下列两个条件: 且
且 =
= +
+ ;②
;② 且
且 =
= .
. 及
及 的坐标;
的坐标;