题目内容
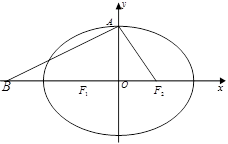
设椭圆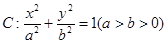 的左、右焦点分别为
的左、右焦点分别为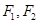 ,
,
上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点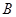 ,满足
,满足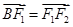 ,且
,且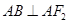 .
.
(Ⅰ)求椭圆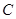 的离心率;
的离心率;
(Ⅱ)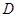 是过
是过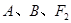 三点的圆上的点,
三点的圆上的点,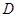 到直线
到直线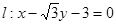 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆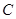 的方程;
的方程;
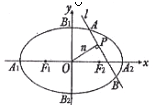
(Ⅲ)在(Ⅱ)的条件下,过右焦点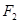 作斜率为
作斜率为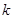 的直线
的直线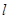 与椭圆
与椭圆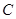 交于
交于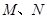 两点,线段
两点,线段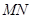 的中垂线与
的中垂线与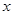 轴相交于点
轴相交于点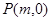 ,求实数
,求实数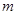 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)
(Ⅱ)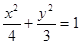 (Ⅲ)
(Ⅲ)
解析试题分析:解:(Ⅰ)连接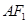 ,因为
,因为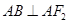 ,
,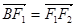 ,所以
,所以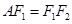 ,
,
即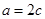 ,故椭圆的离心率
,故椭圆的离心率 .
.
(Ⅱ)由(1)知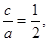 得
得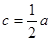 于是
于是 ,
, 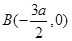 ,
,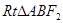 的外接圆圆心为
的外接圆圆心为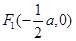 ),半径
),半径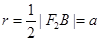
 到直线
到直线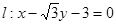 的最大距离等于
的最大距离等于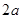 ,所以圆心到直线的距离为
,所以圆心到直线的距离为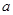 ,
,
所以 ,得
,得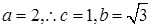 ,椭圆方程为
,椭圆方程为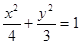
(Ⅲ)由(Ⅱ)知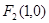 ,
,  :
: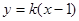
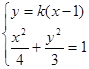 代入消
代入消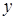 得
得 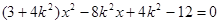
因为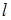 过点
过点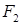 ,所以
,所以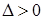 恒成立
恒成立
设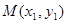 ,
,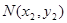 则
则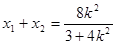 ,
,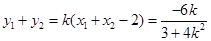
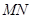 中点
中点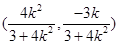
当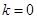 时,
时,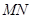 为长轴,中点为原点,则
为长轴,中点为原点,则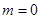
当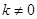 时
时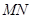 中垂线方程
中垂线方程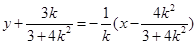 .
.
令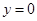 ,
,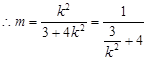
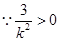 ,
, , 可得
, 可得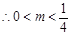
综上可知实数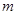 的取值范围是
的取值范围是 .
.
考点:椭圆的方程;椭圆的性质;
点评:关于曲线的大题,难度相对都较大。对于题目涉及到关于直线和其他曲线的交点时,一般都可以用到跟与系数的关系式:在一元二次方程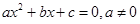 中,
中,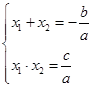 。
。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
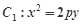 的焦点在抛物线
的焦点在抛物线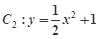 上.
上.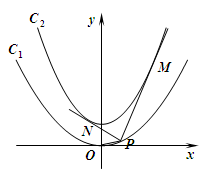
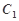 的方程及其准线方程;
的方程及其准线方程;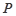 作抛物线
作抛物线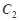 的两条切线
的两条切线 、
、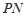 , 切点为
, 切点为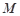 、
、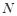 .若
.若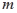 ,且
,且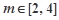 ,求
,求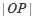 的取值范围.
的取值范围.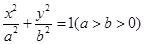 的离心率为
的离心率为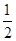 ,右焦点到直线
,右焦点到直线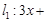
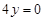 的距离为
的距离为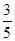 .
.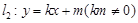 与椭圆C交于A、B两点,且线段AB中点恰好在直线
与椭圆C交于A、B两点,且线段AB中点恰好在直线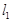 上,求△OAB的面积S的最大值.(其中O为坐标原点).
上,求△OAB的面积S的最大值.(其中O为坐标原点).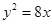 的焦点为右焦点,且经过点A(2,3).
的焦点为右焦点,且经过点A(2,3). 分别为椭圆的左右焦点,求
分别为椭圆的左右焦点,求 的角平分线所在直线的方程.
的角平分线所在直线的方程.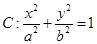 的顶点为
的顶点为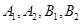 ,焦点为
,焦点为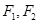 ,
,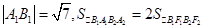 .
. 
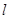 是与n垂直相交于P点,与椭圆相交于A, B两点的直线,
是与n垂直相交于P点,与椭圆相交于A, B两点的直线,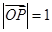 .是否存在上述直线
.是否存在上述直线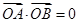 成立?若存在,求出直线
成立?若存在,求出直线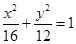 上找一点,使这一点到直线
上找一点,使这一点到直线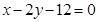 的距离为最小,并求最小值。
的距离为最小,并求最小值。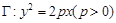 的焦点与椭圆
的焦点与椭圆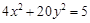 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线 的方程;
的方程; 恒过点
恒过点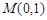 与抛物线
与抛物线 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.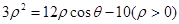
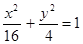 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值 中,一直角三角形
中,一直角三角形 ,
,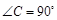 ,B、D在
,B、D在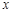 轴上且关于原点
轴上且关于原点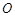 对称,
对称,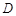 在边
在边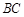 上,BD=3DC,△ABC的周长为12.若一双曲线
上,BD=3DC,△ABC的周长为12.若一双曲线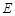 以B、C为焦点,且经过A、D两点.
以B、C为焦点,且经过A、D两点.
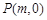 (
(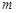 为非零常数)的直线
为非零常数)的直线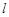 与双曲线
与双曲线 、
、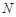 ,且
,且 ,问在
,问在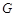 ,使
,使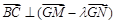 ?若存在,求出所有这样定点
?若存在,求出所有这样定点