题目内容
已知关于x的函数f(x)=x2+2ax+b(其中a,b∈R).
(1)求函数|f(x)|的单调区间;
(2)对于一切a∈[0,1],若存在实数m,使得 与
与 能同时成立,求b-a的取值范围.
能同时成立,求b-a的取值范围.
解:(1)∵f(x)=x2+2ax+b=(x+a)2+a2-b
∴①当a2-b≥0时,单调区间为:(-∞,-a]上为减,[-a,+∞)上为增;(2分)
②当a2-b<0时,单调区间为: 减,
减,
 增,
增, 减,
减, 增(5分)
增(5分)
(2)①当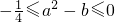 时,由方程
时,由方程 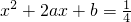 ,解得
,解得  ,
,
此时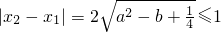 ,此时不满足存在实数m,使得
,此时不满足存在实数m,使得 与
与 能同时成立.(8分)
能同时成立.(8分)
②当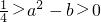 时,由方程
时,由方程 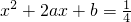 ,解得
,解得 
此时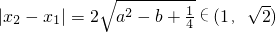 ,满足存在实数m,使得
,满足存在实数m,使得 与
与 能同时成立.(11分),此时有
能同时成立.(11分),此时有 ,故
,故 对一切a∈[0,1]都成立,由此解得b-a∈[-
对一切a∈[0,1]都成立,由此解得b-a∈[- ,-
,- ]
]
③当 时,对一切a∈[0,1],都不存在实数m,使得
时,对一切a∈[0,1],都不存在实数m,使得 与
与 能同时成立.
能同时成立.
综上得b-a∈[- ,-
,- ](16分)
](16分)
分析:(1)f(x)=(x+a)2+a2-b开口向上,但a2-b的正负不定,所以在取绝对值时要分类讨论.在每一种情况下分别求|f(x)|的单调区间.
(2)存在实数m,使得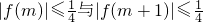 同时成立,即为两变量对应的函数值都小于等于
同时成立,即为两变量对应的函数值都小于等于  的两变量之间间隔不超过1,故须对a2-b和
的两变量之间间隔不超过1,故须对a2-b和  ,
, 的大小分情况讨论,求出a2-b的取值范围,进而求得b-a的取值范围.
的大小分情况讨论,求出a2-b的取值范围,进而求得b-a的取值范围.
点评:点评:本题考查了数学上的分类讨论思想.分类讨论目的是,分解问题难度,化整为零,各个击破.
∴①当a2-b≥0时,单调区间为:(-∞,-a]上为减,[-a,+∞)上为增;(2分)
②当a2-b<0时,单调区间为:
 减,
减, 增,
增, 减,
减, 增(5分)
增(5分)(2)①当
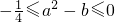 时,由方程
时,由方程 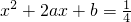 ,解得
,解得  ,
,此时
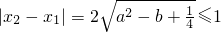 ,此时不满足存在实数m,使得
,此时不满足存在实数m,使得 与
与 能同时成立.(8分)
能同时成立.(8分)②当
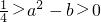 时,由方程
时,由方程 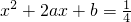 ,解得
,解得 
此时
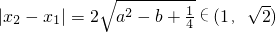 ,满足存在实数m,使得
,满足存在实数m,使得 与
与 能同时成立.(11分),此时有
能同时成立.(11分),此时有 ,故
,故 对一切a∈[0,1]都成立,由此解得b-a∈[-
对一切a∈[0,1]都成立,由此解得b-a∈[- ,-
,- ]
]③当
 时,对一切a∈[0,1],都不存在实数m,使得
时,对一切a∈[0,1],都不存在实数m,使得 与
与 能同时成立.
能同时成立.综上得b-a∈[-
 ,-
,- ](16分)
](16分)分析:(1)f(x)=(x+a)2+a2-b开口向上,但a2-b的正负不定,所以在取绝对值时要分类讨论.在每一种情况下分别求|f(x)|的单调区间.
(2)存在实数m,使得
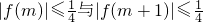 同时成立,即为两变量对应的函数值都小于等于
同时成立,即为两变量对应的函数值都小于等于  的两变量之间间隔不超过1,故须对a2-b和
的两变量之间间隔不超过1,故须对a2-b和  ,
, 的大小分情况讨论,求出a2-b的取值范围,进而求得b-a的取值范围.
的大小分情况讨论,求出a2-b的取值范围,进而求得b-a的取值范围.点评:点评:本题考查了数学上的分类讨论思想.分类讨论目的是,分解问题难度,化整为零,各个击破.

练习册系列答案
相关题目