Question

若两个等差数列的前n项和之比是(7n+1)∶(4n+27),试求它们的第11项之比.

Answer 1

思路分析:本题主要考查等差数列的性质及前n项和公式.本题可以采用基本量法或结合函数性质及前n项和公式S_n=来求解.

解法一(利用基本量法):设两个等差数列的公差分别为d₁、d₂,首项分别为a₁、b₁,前n项和分别为S_n、S_n′,则==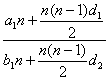=.于是=,=,且=,于是a₁=d₁,b₁=d₂,

∴====.

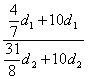    解法二(利用等差数列的性质):设数列{a_n}的前n项和为S_n,数列{b_n}的前n项和为S_n′,

    则有a₁₁=,b₁₁=,

    所以=====.

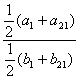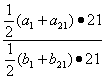    解法三(利用等差数列前n项和是关于n的二次函数解题):令S_n=(7n+1)·nk,S_n′=(4n+27)·nk,

    由a_n=S_n-S_n-1=k(14n-6),得a₁₁=148k,

    由b_n=S_n′-S_n-1′=k(8n+23),得b₁₁=111k,

    所以==.

    思维启示:(1)解法一是运用基本量法;解法二关键抓住了等差数列的通项与前n项和之间的关系;解法三利用了等差数列的函数特性.三种方法均具一般性.

(2)==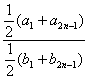=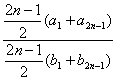,于是=.

(3)错解:由于=,于是设S_n=(7n+1)k,S_n′=(4n+27)k,则有a₁₁=S₁₁-S₁₀=(7×11+1)k-(7×10+1)k=7k,b₁₁=S₁₁′-S₁₀′=(4×11+27)k-(4×10+27)k=4k,

∴==.

    错因分析:该解法错误的原因是没有搞清楚等差数列前n项和的形式,它应是关于n的二次函数形式An²+Bn(A、B是常数),而不是一次函数形式,同学们解题时,一定要考虑a_n,S_n的表达形式.