题目内容
已知p:函数 有两个零点,.若
有两个零点,.若 为真,
为真, 为假,则实数m的取值范围为( )
为假,则实数m的取值范围为( )
A. | B. |
C. | D. |
B
解析试题分析:解:∵ 为真,
为真, 为假,∴p,q是一个真命题,一个假命题,由p:函数f(x)=x2+mx+1有两个零点,得△=m2-4>0,解得m>2或m<-2.由q:
为假,∴p,q是一个真命题,一个假命题,由p:函数f(x)=x2+mx+1有两个零点,得△=m2-4>0,解得m>2或m<-2.由q: ,
, ,得△=16(m-2)2-16<0,解得1<m<3,∴实数m的取值范围为
,得△=16(m-2)2-16<0,解得1<m<3,∴实数m的取值范围为 ,故选B.
,故选B.
考点:命题的真值
点评:解决的关键是利用函数的零点的概念来分析得到,以及全称命题的理解和运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若 表示直线,
表示直线, 表示平面,且
表示平面,且 ,则“
,则“ ”是“
”是“ ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
在四边形ABCD中,“ ,且
,且 ”是“四边形ABCD是菱形”的
”是“四边形ABCD是菱形”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知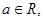 则
则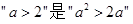 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
已知 ,函数
,函数 ,向量
,向量 与向量
与向量 垂直时,则下列选项的命题中为假命题的是( )
垂直时,则下列选项的命题中为假命题的是( )
A. | B. |
C. | D. |
“1≤x≤4”是“1≤x2≤16”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知函数 ,则“
,则“ ”是“函数
”是“函数 在R上递增”的( )
在R上递增”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若ab=0,则a=0或b=0”的逆否命题是 ( )
| A.若ab≠0,则a≠0或b≠0 | B.若a≠0或b≠0,则ab≠0 |
| C.若ab≠0,则a≠0且b≠0 | D.若a≠0且b≠0,则ab≠0 |
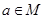 则
则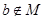 ”的逆否命题是 ( )
”的逆否命题是 ( )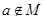 ,则
,则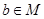 D、若
D、若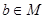 ,则
,则