题目内容
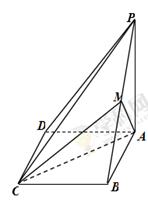
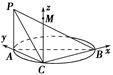
如图,在四棱锥 中,
中, 为平行四边形,且
为平行四边形,且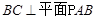 ,
, ,
,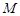 为
为 的中点,
的中点,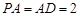 ,
,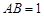 .
.
(Ⅰ)求证: //
//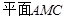 ;
;
(Ⅱ)求三棱锥 的高.
的高.
(Ⅰ)详见解析;(Ⅱ) .
.
解析试题分析:(Ⅰ)连接 ,设
,设 与
与 相交于点
相交于点 ,连接
,连接 ,根据
,根据 为
为 的中位线便可得出结论;(Ⅱ)由条件证明
的中位线便可得出结论;(Ⅱ)由条件证明 ,
, ,再 利用等体积法求得,即
,再 利用等体积法求得,即 .
.
试题解析:
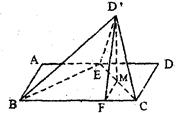
(Ⅰ)证明:连接 ,设
,设 与
与 相交于点
相交于点 ,连接
,连接 ,
,
∵ 四边形 是平行四边形,∴点
是平行四边形,∴点 为
为 的中点.
的中点.
∵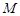 为
为 的中点, ∴
的中点, ∴ 为
为 的中位线,
的中位线,
∴ . 2分
. 2分
∵ ,
,
∴ //
//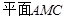 . 4分
. 4分
(Ⅱ)解:∵ 平面
平面 ,
, ,
,
则 平面
平面 ,故
,故 ,
,
又 , 且
, 且 ,
,
∴ . 8分
. 8分
取 的中点
的中点 ,连接
,连接 ,则
,则 ,
,
∴ ,且
,且 . 9分
. 9分
设三棱锥 的高为
的高为 ,由
,由 ,
,
有 ,得
,得 . 12分
. 12分
考点:四棱锥的性质,空间中的线线平行与垂直,线面平行与垂直,二面角.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
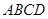 ,
,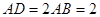 ,点
,点 是
是 的中点,将△
的中点,将△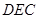 沿
沿 折起到△
折起到△ 的位置,使二面角
的位置,使二面角 是直二面角.
是直二面角.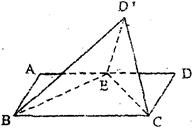
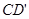 ⊥面
⊥面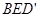 ;
;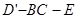 的余弦值.
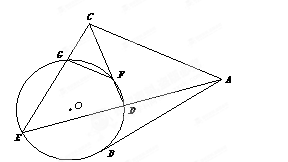
的余弦值.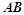 是⊙
是⊙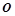 的一条切线,切点为
的一条切线,切点为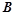 ,
,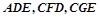 都是⊙
都是⊙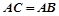 .
.
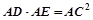 ;
;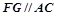 .
.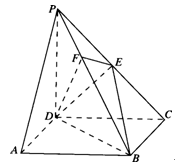
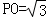 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.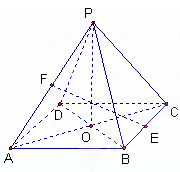
 中,
中, 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面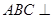 平面
平面 ,
, .
.
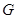 是
是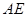 的中点,求证:
的中点,求证: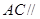 平面
平面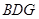 ;
;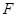 在线段
在线段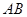 上什么位置时,二面角
上什么位置时,二面角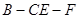 的余弦值为
的余弦值为 .
.
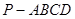 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点.
,E是PC的中点.
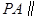 平面EDB;
平面EDB; 中,底面
中,底面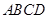 为平行四边形,侧面
为平行四边形,侧面 底面
底面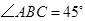 ,
,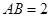 ,
,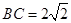 ,
,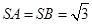 .
.
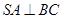 ;
;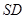 与平面
与平面 所成角的正弦值.
所成角的正弦值.