题目内容
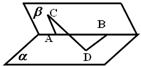
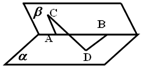如图，60°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直AB，已知AB=4，AC=6，BD=8，求CD的长．分析：利用已知条件确定＜
，
＞的值，利用|
|2=(
+
+
)2，通过向量的数量积的运算求出CD的距离．
| CA |
| BD |
| CD |
| CA |
| AB |
| BD |
解答：解：由已知，可得AC⊥AB，BD⊥AB
所以＜
，
＞=120°，…（4分）
∴|
|2=(
+
+
)2
=|
|2+|
|2+|
|2+2
•
+2
•
+2
•
…（8分）
=36+16+64+2×6×8×cos120°=68．
∴CD=
=2
． …（10分）
（其他解法酌情给分）
所以＜
| CA |
| BD |
∴|
| CD |
| CA |
| AB |
| BD |
=|
| CA |
| AB |
| BD |
| CA |
| AB |
| CA |
| BD |
| AB |
| BD |
=36+16+64+2×6×8×cos120°=68．
∴CD=
| 68 |
| 17 |
（其他解法酌情给分）
点评：本题考查空间两点间的距离的求法，空间向量的数量积的应用，注意二面角的范围的应用，考查计算能力．
练习册系列答案
相关题目
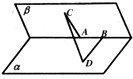如图，60°的二面角的棱上有A、B两点，线段AC、BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，则CD的长为（ ）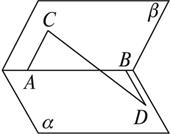
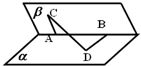β,BD
α,AC⊥AB于A,BD⊥AB于B,且AC=AB=BD=1,则CD的长为… ( )
C.2 D.
如图，60°的二面角的棱上有A、B两点，直线AC、BD分别在这个二面角的两个半平面内，且都垂直AB，已知AB=4，AC=6，BD=8，求CD的长．