题目内容
抛物线y=2bx2的焦点坐标是
- A.(0,
 )
) - B.(0,
 )
) - C.(
 ,0)
,0) - D.(
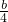 ,0)
,0)
B
分析:将抛物线y=2bx2的方程化为标准方程x2= y后,根据抛物线的性质,即可得到其焦点坐标.
y后,根据抛物线的性质,即可得到其焦点坐标.
解答:抛物线y=2bx2的方程可化为:
x2= y
y
当b<0时
其焦点坐标为:(0, )
)
同理:当b>0时,焦点坐标为:(0, )
)
综上所述抛物线y=2bx2的焦点坐标为(0, )
)
故选B.
点评:题考查的知识点是抛物线的简单性质,其中将抛物线方程化为标准方程是解答本题关键.
分析:将抛物线y=2bx2的方程化为标准方程x2=
 y后,根据抛物线的性质,即可得到其焦点坐标.
y后,根据抛物线的性质,即可得到其焦点坐标.解答:抛物线y=2bx2的方程可化为:
x2=
 y
y当b<0时
其焦点坐标为:(0,
 )
)同理:当b>0时,焦点坐标为:(0,
 )
)综上所述抛物线y=2bx2的焦点坐标为(0,
 )
)故选B.
点评:题考查的知识点是抛物线的简单性质,其中将抛物线方程化为标准方程是解答本题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
抛物线y=2bx2的焦点坐标是( )
A、(0,
| ||
B、(0,
| ||
C、(
| ||
D、(
|
 )
) )
) ,0)
,0) ,0)
,0) )
) )
) ,0)
,0) ,0)
,0)