题目内容
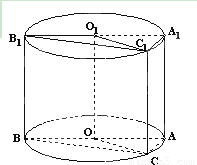
 如图,轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.∠AOC=60°
如图,轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.∠AOC=60°(1)求三棱柱AOC-A1O1C1的体积;
(2)证明:平面AA1C1C⊥平面BB1C1C.
分析:(1)求得S△AOC,利用棱柱的体积公式计算即可;
(2)可先证得BC⊥面AA1C1C,再利用面面垂直的判定定理即可证得.
(2)可先证得BC⊥面AA1C1C,再利用面面垂直的判定定理即可证得.
解答:解:(1)由题意知AO=OC=1,又∠AOC=60°,
∴S△AOC=
•AO•OC•sin60°=
,
又三棱柱AOC-A1O1C1的高h=AA1=2,设三棱柱AOC-A1O1C1的体积为V,
则V=S△AOC•AA1=
•2=
;
(2)∵AA1⊥BC,AC⊥BC,
∴BC⊥面AA1C1C,
又BC?平面BB1C1C,
∴面AA1C1C⊥平面BB1C1C.
∴S△AOC=
| 1 |
| 2 |
| ||
| 4 |
又三棱柱AOC-A1O1C1的高h=AA1=2,设三棱柱AOC-A1O1C1的体积为V,
则V=S△AOC•AA1=
| ||
| 4 |
| ||
| 2 |
(2)∵AA1⊥BC,AC⊥BC,
∴BC⊥面AA1C1C,
又BC?平面BB1C1C,
∴面AA1C1C⊥平面BB1C1C.
点评:本题考查直线与平面垂直的判定,考查棱柱的体积,突出考查分析与证明的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心.
如图,已知圆锥的轴截面ABC是边长为2的正三角形,O是底面圆心. 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径.
的直径.
 的体积;
的体积; ⊥平面
⊥平面

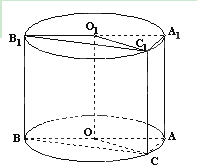 如图,轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.∠AOC=60°
如图,轴截面为边长是2的正方形的圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.∠AOC=60°