题目内容

已知函数f(n)=n2cos(nπ),且an=f(n)+f(n+1),则a1+a2+a3+…+a100=(　　)

A.0                 B.-100

C.100                   D.10 200

B.因为f(n)=n2cos(nπ),

所以a1+a2+a3+…+a100=[f(1)+f(2)+…+f(100)]+[f(2)+…+f(101)],

f(1)+f(2)+…+f(100)

=-12+22-32+42-…-992+1002

=(22-12)+(42-32)+…+(1002-992)

=3+7+…+199

==5 050,

f(2)+…+f(101)

=22-32+42-…-992+1002-1012

=(22-32)+(42-52)+…+(1002-1012)

=-5-9-…-201==-5 150,

所以a1+a2+a3+…+a100

=[f(1)+f(2)+…+f(100)]+[f(2)+…+f(101)]

=-100.

练习册系列答案
相关题目
已知函数f（x）=x-2
2x
+2（x≥2）
（Ⅰ）求反函数；
（Ⅱ）若数列{an}（an＞0）的前n项和Sn=f-1（Sn-1），（x≥2），且a1=2求数列{an}的通项公式；
（Ⅲ） 令bn=
an+1 -an 
2anan+1
（n∈N），求
lim
n→∞
(b1+b2+…+bn-n)．
已知函数f（x）=ax+lnx，a∈R．
（I）当a=-1时，求f（x）的最大值；
（II）对f（x）图象上的任意不同两点P1（x1，x2），P（x2，y2）（0＜x1＜x2），证明f（x）图象上存在点P0（x0，y0），满足x1＜x0＜x2，且f（x）图象上以P0为切点的切线与直线P1P2平等；
（III）当a=
32
时，设正项数列{an}满足：an+1=f'（an）（n∈N*），若数列{a2n}是递减数列，求a1的取值范围．

已知函数f(x)＝x2－ax＋b·(a，b∈R)的图像经过坐标原点，且(1)＝1，数列{an}的前n项和Sn＝f(n)(n∈N*)．

(Ⅰ)求数列{an}的通项公式；

(Ⅱ)若数列{bn}满足lon3bn＝an+1＋log3n，求数列{bn}的前n项和．
已知函数f（x）=ax+lnx，a∈R．
（I）当a=-1时，求f（x）的最大值；
（II）对f（x）图象上的任意不同两点P1（x1，x2），P（x2，y2）（0＜x1＜x2），证明f（x）图象上存在点P0（x0，y0），满足x1＜x0＜x2，且f（x）图象上以P0为切点的切线与直线P1P2平等；
（III）当a=
3
2
时，设正项数列{an}满足：an+1=f'（an）（n∈N*），若数列{a2n}是递减数列，求a1的取值范围．
已知函数f（x）=ax2+bx（a≠0）的导函数f'（x）=-4x+22，数列{an}的前n项和为Sn，点Pn（n，Sn）（n∈N*）均在函数y=f（x）的图象上．
（Ⅰ）求数列{an}的通项公式an及前n项和Sn；
（Ⅱ）存在k∈N*，使得对任意n∈N*恒成立，求出k的最小值；
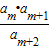（Ⅲ）是否存在m∈N*，使得为数列{an}中的项？若存在，求出m的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网