题目内容
两圆内切于点P,大圆的弦AD交小圆于点B、C.求证:∠APB=∠CPD.
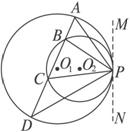
图
证明:过P作两圆的公切线MN.
∵PB是小圆弦,MN是切线,∴∠BPM=∠BCP.
∵PA是大圆弦,MN是切线,
∴∠APM=∠D.
∴∠BPM-∠APM=∠BCP-∠D.
又∠BCP=∠D+∠CPD,∴∠BCP-∠D=∠CPD.
∴∠APB=∠CPD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
两圆内切于点P,大圆的弦AD交小圆于点B、C.求证:∠APB=∠CPD.

图
证明:过P作两圆的公切线MN.
∵PB是小圆弦,MN是切线,∴∠BPM=∠BCP.
∵PA是大圆弦,MN是切线,
∴∠APM=∠D.
∴∠BPM-∠APM=∠BCP-∠D.
又∠BCP=∠D+∠CPD,∴∠BCP-∠D=∠CPD.
∴∠APB=∠CPD.

 名校课堂系列答案
名校课堂系列答案