题目内容
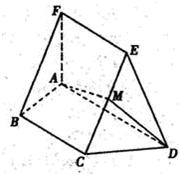（2010•淄博一模）如图，在五面体ABCDEF中，FA⊥平面ABCD，AD∥BC∥FE，AB⊥AD，M为EC的中点，AF=AB=BC=FE=| 1 | 2 |
（1）求证：BF⊥DM
（2）求平面AMD⊥平面CDE．
分析：（1）设P为AD的中点，连接EP，PC，所以EF
AP
BC，所以FA∥EP，可得EP⊥平面ABCD，所以EP⊥PC，EP⊥AD，再结合直角三角形的性质可得：ED=CD，进而得到：DM⊥CE，又BF∥EC，所以DM⊥BF．
（2）欲证平面AMD⊥平面CDE，即证CE⊥平面AMD，根据线面垂直的判定定理可知只需证CE与平面AMD内两相交直线垂直即可，易证DM⊥CE，MP⊥CE．
| ||
. |
| ||
. |
（2）欲证平面AMD⊥平面CDE，即证CE⊥平面AMD，根据线面垂直的判定定理可知只需证CE与平面AMD内两相交直线垂直即可，易证DM⊥CE，MP⊥CE．
解答：解：（1）证明：设P为AD的中点，连接EP，PC，
所以由已知，EF
AP
BC
∴EP=PC，FA∥EP，EC∥BF，AB∥PC…（2分）
又∵FA⊥平面ABCD，
∴EP⊥平面ABCD
因为PC、AD?平面ABCD
所以EP⊥PC，EP⊥AD
设FA=a，则EP=PC=PD=a，
∴ED=CD=
a…（5分）
∵M为EC的中点，
∴DM⊥CE
∵BF∥EC
∴DM⊥BF．…（6分）
（2）证明：连接MP
∵PE=PC，M为EC的中点，∴MP⊥CE
又DM⊥CE，MP∩DM=M
故CE⊥平面AMD…（10分）
而CE?平面CDE．
∴平面AMD⊥平面CDE．…（12分）
所以由已知，EF
| ||
. |
| ||
. |
∴EP=PC，FA∥EP，EC∥BF，AB∥PC…（2分）
又∵FA⊥平面ABCD，
∴EP⊥平面ABCD
因为PC、AD?平面ABCD
所以EP⊥PC，EP⊥AD
设FA=a，则EP=PC=PD=a，
∴ED=CD=
| 2 |
∵M为EC的中点，
∴DM⊥CE
∵BF∥EC
∴DM⊥BF．…（6分）
（2）证明：连接MP
∵PE=PC，M为EC的中点，∴MP⊥CE
又DM⊥CE，MP∩DM=M
故CE⊥平面AMD…（10分）
而CE?平面CDE．
∴平面AMD⊥平面CDE．…（12分）
点评：本小题要考查线面垂直、平面与平面垂直等基础知识，考查空间想像能力和推理论证能力．
练习册系列答案
相关题目