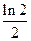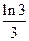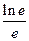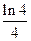题目内容
(本题10分)
已知函数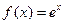 (
(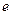 是自然对数的底数,
是自然对数的底数,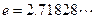 ).
).
(I)证明:对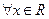 ,不等式
,不等式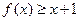 恒成立;
恒成立;
(II)数列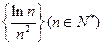 的前
的前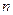 项和为
项和为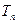 ,求证:
,求证: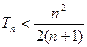 .
.
已知函数
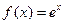 (
(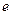 是自然对数的底数,
是自然对数的底数,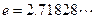 ).
).(I)证明:对
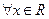 ,不等式
,不等式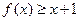 恒成立;
恒成立;(II)数列
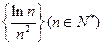 的前
的前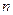 项和为
项和为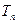 ,求证:
,求证: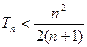 .
.解:(I)设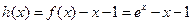
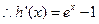 ,当
,当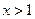 时,
时, 函数
函数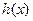 单调递增;
单调递增;
当 时,
时, ,函数
,函数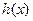 单调递减. 当
单调递减. 当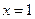 时,
时,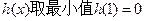 .
.
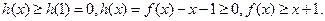
(II)由(I)可知,对任意的实数 ,不等式
,不等式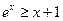 恒成立,设
恒成立,设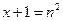
所以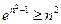 ,
,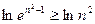 ,即
,即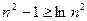 ,
,
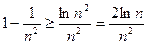 ,
,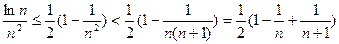

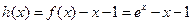
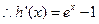 ,当
,当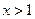 时,
时, 函数
函数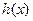 单调递增;
单调递增;当
 时,
时, ,函数
,函数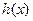 单调递减. 当
单调递减. 当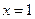 时,
时,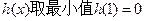 .
. | (-∞,1) | 1 | (1,+∞) |
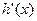 | - | 0 | + |
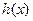 | 递减 | 极小值 | 递增 |
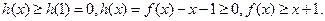
(II)由(I)可知,对任意的实数
 ,不等式
,不等式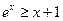 恒成立,设
恒成立,设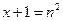
所以
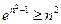 ,
,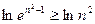 ,即
,即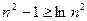 ,
,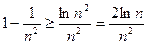 ,
,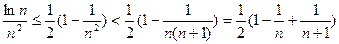

略

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 的前
的前 项和为
项和为 ,且对于任意
,且对于任意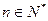 ,都有
,都有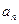 是
是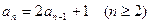 ;
;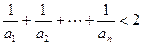 .
.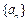 的公比为q,第8项是第2项与第5项的等差中项.
的公比为q,第8项是第2项与第5项的等差中项.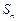 ,判断
,判断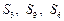 是否成等差数列,并说明理由.
是否成等差数列,并说明理由.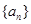 的通项为
的通项为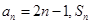 为数列
为数列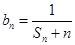 ,则数列
,则数列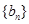 的前n项和的取值范围为( )
的前n项和的取值范围为( )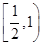
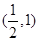


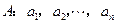 ,若满足
,若满足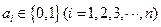 ,则称数列
,则称数列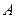 为“0-1数列”.定义变换
为“0-1数列”.定义变换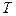 ,
,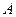 :1,0,1,则
:1,0,1,则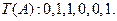 设
设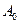 是“0-1数列”,令
是“0-1数列”,令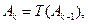
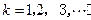 .
.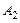 :
: 求数列
求数列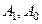 ;
;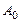 共有10项,则数列
共有10项,则数列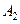 中连续两项相等的数对至少有多少对?请说明理由;
中连续两项相等的数对至少有多少对?请说明理由;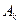 中连续两项都是0的数对个数为
中连续两项都是0的数对个数为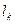 ,
,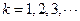 .求
.求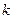 的表达式.
的表达式.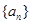 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列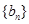 的首项为
的首项为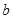 ,公比为a,其中
,公比为a,其中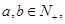 且
且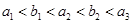 ,则a的值为 ( )
,则a的值为 ( )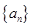 和
和 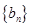 的前n项和分别为
的前n项和分别为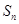 和
和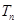 ,且
,且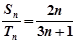 ,则
,则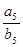 = ( )
= ( )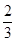
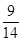
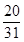
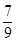
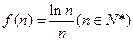 的最大值为 ( )
的最大值为 ( )