题目内容
 已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=
已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC= ,CD=1,则这个三棱锥外接球的表面积是 ________(结果可含π)
,CD=1,则这个三棱锥外接球的表面积是 ________(结果可含π)

分析:如图所示,取AD中点E,则CE、BE为折线,三角形BEC为底面三角形,通过计算说明∠ECB=90°,∠PCB=90°,故各平面三角形都有一个直角.BE的中点为O,就是外接球的球心,OE就是半径,求出半径,即可求出球的表面积.
解答:如图所示,取AD中点E,则CE、BE为折线,三角形BEC为底面三角形,AB=2,BC=
 ,CD=1
,CD=1AD=
 ,DE=
,DE= ,CE=
,CE= ,
,BE=

CE2+BC2=
 ,BE2=
,BE2= ,
,CE2+BC2=BE2,
∠ECB=90°,
按折线折起后,三角形PCB,PC=CD=1,PB=AB=2,BC=
 ,
,

∠PCB=90°,
故各平面三角形都有一个直角.
BE的中点为O,就是外接球的球心,OE就是半径:
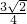
外接球的表面积为:
 =
=
故答案为:

点评:本题是中档题,考查空间想象能力,逻辑思维能力,以及计算能力,作图能力,合理选择折线是解好本题的突破口、关键点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
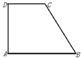 已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=
已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC= (2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )
(2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )
 ,CD=1,则这个三棱锥外接球的表面积是 (结果可含π)
,CD=1,则这个三棱锥外接球的表面积是 (结果可含π)