题目内容

将(1+x-2x2)5展开后,按x的升幂排列得多项式f(x)=a0+a1x+a2x2+…+anxn,求a4的值.

解析：∵(1+x-2x2)5=［1+x(1-2x)］5,通项Tr+1=xr(1-2x)r，该通项的通项为(-2)kxr+k，其中0≤r≤5，0≤k≤r.

令r+k=4,∴

∴x4的系数a4为+(-2)+ (-2)2=-15.

练习册系列答案
相关题目
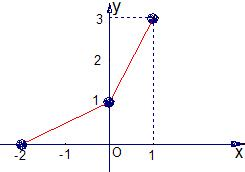精英家教网在同一平面直角坐标系中，函数y=f（x）和y=g（x）的图象关于直线y=x对称．现将y=g（x）的图象沿x轴向左平移2个单位，再沿y轴向上平移1个单位，所得的图象是由两条线段组成的折线（如图所示），则函数f（x）的表达式为（　　）
A、f（x）=
2x+2，-1≤x≤0
x
2
+2，0＜x≤2
B、f（x）=
2x-2，-1≤x≤0
x
2
-2，0＜x≤2
C、f（x）=
2x-2，1≤x≤2
x
2
+1，2＜x≤4
D、f（x）=
2x-6，1≤x≤2
x
2
-3，2＜x≤4
已知两组数据x1，x2，…，xn与y1，y2，…，yn，它们的平均数分别是
.
x
和
.
y
，则新的一组数据2x1-3y1+1，2x2-3y2+1，…，2xn-3yn+1的平均数是
 
．在总体中抽取了一个样本，为了便于统计，将样本中的每个数据乘以100后进行分析，得出新样本平均数为3，则估计总体的平均数为
 
．
将函数y=2x2向左平移一个单位，再向上平移3个单位后可以得到（　　）
将多项式x3+2x2+x-1用秦九韶算法求值时，其表达式应写成
（（x+2）x+1）x-1
（（x+2）x+1）x-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网