题目内容
如图,PA=BC=6,AC=8,PC=AB=10,PB=2
思路点拨:本题要证明线面垂直关系,可以紧紧围绕着线面垂直的判定定理来考虑,去证明相关的线线垂直.由于已知条件中出现了一些线段的长度,因此可以考虑利用勾股定理的逆定理来判定,从而得证.
证明:∵PA2+AC2=36+64=100=PC2,
∴△PAC是以∠PAC为直角的直角三角形.
同理可证△PAB是以∠PAB为直角的直角三角形.△PCB是以∠PCB为直角的直角三角形.故PA⊥平面ABC.
又∵S△PBC=![]() |AC||BC|
|AC||BC|
=![]() ×10×6=30,
×10×6=30,
而![]() |PB||CF|=
|PB||CF|=![]() ×2
×2![]() ×
×![]() =30=S△PBC,故CF⊥PB.
=30=S△PBC,故CF⊥PB.
又已知EF⊥PB,
∴PB⊥平面CEF.
[一通百通] 有关证明线面垂直的问题,通常可以围绕着线面垂直的判定定理来考虑,从而将问题转化为线线垂直的问题,如果已知条件中出现了有关的线段的长度时,常常要考虑利用勾股定理的逆定理来判定相关的角是直角,从而将问题解决.

练习册系列答案
相关题目
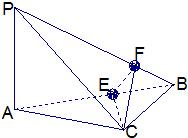 如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2,
 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.