题目内容
比较下列各组数的大小
（1）sin 1，sin
；
（2）cos
，cos
；
（3）sin110°，sin150°．
（1）sin 1，sin
| π |
| 3 |
（2）cos
| 4 π |
| 7 |
| 5 π |
| 7 |
（3）sin110°，sin150°．
考点：正弦函数的图象
专题：三角函数的求值
分析：（1）根据函数y=sinx在（0，
）上是增函数，可得sin 1＜sin
．
（2）利用函数y=cosx在（0，π）上是减函数，可得cos
＞cos
．
（3）利用诱导公式以及函数y=sinx在（0°，90°）上是增函数，可得sin 70°＞sin30°，从而得出结论．
| π |
| 2 |
| π |
| 3 |
（2）利用函数y=cosx在（0，π）上是减函数，可得cos
| 4 π |
| 7 |
| 5 π |
| 7 |
（3）利用诱导公式以及函数y=sinx在（0°，90°）上是增函数，可得sin 70°＞sin30°，从而得出结论．
解答：
解：（1）∵1、
∈（0，
），1＜
，函数y=sinx在（0，
）上是增函数，
故有sin 1＜sin
．
（2）∵
、
∈（0，π），函数y=cosx在（0，π）上是减函数，
故有 cos
＞cos
．
（3）∵sin110°=sin70°，sin150°=sin30°，函数y=sinx在（0°，90°）上是增函数，
故有sin 70°＞sin30°，即 sin110°＞sin150°．
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
故有sin 1＜sin
| π |
| 3 |
（2）∵
| 4π |
| 7 |
| 5π |
| 7 |
故有 cos
| 4 π |
| 7 |
| 5 π |
| 7 |
（3）∵sin110°=sin70°，sin150°=sin30°，函数y=sinx在（0°，90°）上是增函数，
故有sin 70°＞sin30°，即 sin110°＞sin150°．
点评：本题主要考查由导公式，正弦函数、余弦函数的单调性的应用，属于基础题．
练习册系列答案
相关题目
直线x=-1的倾斜角是（ ）
| A、0° | B、45° |
| C、135° | D、90° |
函数f（x）=2sin（
x-
）的图象为C
①图象C关于直线x=2π对称；
②f（x）在区间（-π，2π）内是增函数；
③由y=2sin
x的图象向右平移
个单位长度可以得到图象C．
以上三个诊断中，正确诊断的个数是（ ）
| 1 |
| 3 |
| π |
| 6 |
①图象C关于直线x=2π对称；
②f（x）在区间（-π，2π）内是增函数；
③由y=2sin
| 1 |
| 3 |
| π |
| 6 |
以上三个诊断中，正确诊断的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
在△ABC中，已知
•
=tanA，当A=
时，△ABC的面积为（ ）
| AB |
| AC |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知等腰三角形的腰长是底边长的2倍，那么它的顶角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
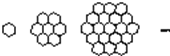蜜蜂被认为是自然界中最杰出的建筑师，单个蜂巢可以近似地看作是一个正六边形，如图为一组蜂巢的截面图．其中第一个图有1个蜂巢，第二个图有7个蜂巢，第三个图有19个蜂巢，按此规律，以f（n）表示第n个图的蜂巢总数．