题目内容
20.设三角形的三条边的长度分别是x,y,$\sqrt{{x}^{2}-xy+{y}^{2}}$,则最大边与最小边的夹角θ=$\frac{π}{3}$.分析 设x>y>0,可得三角形的三边关系是:x>$\sqrt{{x}^{2}-xy+{y}^{2}}$>y>0,利用余弦定理即可求得cosθ=$\frac{1}{2}$,结合角的范围,即可解得夹角θ的值.
解答 解:设x>y>0,
1、x>y>0,
xy>y2,
0>-xy+y2,
x2>x2-xy+y2
x>$\sqrt{{x}^{2}-xy+{y}^{2}}$;
2、x>y>0,
x2>xy,
x2-xy>0,
x2-xy+y2>y2,
$\sqrt{{x}^{2}-xy+{y}^{2}}$>y,
综上可得:三角形的三边关系是:x>$\sqrt{{x}^{2}-xy+{y}^{2}}$>y>0
那么最长边与最短边的夹角就是x与y的夹角
cosθ=$\frac{{x}^{2}+{y}^{2}-{x}^{2}+xy-{y}^{2}}{2xy}$=$\frac{1}{2}$,故解得:夹角θ是$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题主要考查了余弦定理在解三角形中的应用,正确判断三角形三边的大小关系是解题的关键,属于中档题.

练习册系列答案
相关题目
11.已知等差数列{an}的公差d=-2,a1+a4+a7+…+a97=50,那么a3+a6+a9+…+a99的值是( )
| A. | -78 | B. | -82 | C. | -148 | D. | -182 |
8.设变量x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y-2≤0}\\{y≤1}\end{array}\right.$,则目标函数z=x+2y的最小值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
5.如图是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )
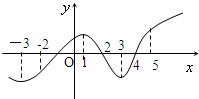
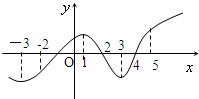
| A. | 在区间(-2,1)上f(x)是增函数 | B. | 当x=4时,f(x)取极大值 | ||
| C. | 在(1,3)上f(x)是减函数 | D. | 在(4,5)上f(x)是增函数 |