题目内容
已知函数 。
。
(1)若 的解集为
的解集为 ,求实数
,求实数 的值。
的值。
(2)当 且
且 时,解关于
时,解关于 的不等式
的不等式 。
。
【答案】
(Ⅰ) . (Ⅱ)当t=0时,原不等式的解集为R,当t>0时,原不等式的解集为
. (Ⅱ)当t=0时,原不等式的解集为R,当t>0时,原不等式的解集为 .
.
【解析】
试题分析:(Ⅰ)由|x﹣a|≤m得a﹣m≤x≤a+m,
所以 解之得
解之得 为所求.
4分
为所求.
4分
(Ⅱ)当a=2时,f(x)=|x﹣2|,
所以f(x)+t≥f(x+2t)?|x﹣2+2t|﹣|x﹣2|≤t,①
当t=0时,不等式①恒成立,即x∈R;
当t>0时,不等式
解得x<2﹣2t或 或x∈?,即
或x∈?,即 ;
;
综上,当t=0时,原不等式的解集为R,
当t>0时,原不等式的解集为 .
10分
.
10分
考点:本题考查了绝对值不等式的解法及恒成立问题的解法
点评:不等式选讲主要考查绝对值不等式的解法、不等式证明及其应用,要求学生学会从分段函数角度来解绝对值不等式及绝对值不等式的最值问题等,掌握常见的证明不等式的方法如综合法、分析法、数学归纳法等。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为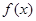 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素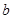 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程