ĢāÄæÄŚČŻ
£Ø2013•½ĖÕŅ»Ä££©£Ø1£©É½Ė®³ĒŹŠÕņ½ÓŠ”°ČżÉ½”±--½šÉ½”¢½¹É½”¢±±¹Ģɽ£¬Ņ»Ī»ÓĪæĶÓĪĄĄÕāČżøö¾°µćµÄøÅĀŹ¶¼ŹĒ0.5£¬ĒŅøĆÓĪæĶŹĒ·ńÓĪĄĄÕāČżøö¾°µćĻą»„¶ĄĮ¢£¬ÓƦĪ±ķŹ¾ÕāĪ»ÓĪæĶÓĪĄĄµÄ¾°µćŹżŗĶƻӊÓĪĄĄµÄ¾°µćŹż²īµÄ¾ų¶ŌÖµ£¬Ēó¦ĪµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£»
£Ø2£©Ä³³ĒŹŠÓŠn£ØnĪŖĘꏿ£¬n”Ż3£©øö¾°µć£¬Ņ»Ī»ÓĪæĶÓĪĄĄĆæøö¾°µćµÄøÅĀŹ¶¼ŹĒ0.5£¬ĒŅøĆÓĪæĶŹĒ·ńÓĪĄĄÕānøö¾°µćĻą»„¶ĄĮ¢£¬ÓƦĪ±ķŹ¾ÕāĪ»ÓĪæĶÓĪĄĄµÄ¾°µćŹżŗĶƻӊÓĪĄĄµÄ¾°µćŹż²īµÄ¾ų¶ŌÖµ£¬Ēó¦ĪµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£®
£Ø2£©Ä³³ĒŹŠÓŠn£ØnĪŖĘꏿ£¬n”Ż3£©øö¾°µć£¬Ņ»Ī»ÓĪæĶÓĪĄĄĆæøö¾°µćµÄøÅĀŹ¶¼ŹĒ0.5£¬ĒŅøĆÓĪæĶŹĒ·ńÓĪĄĄÕānøö¾°µćĻą»„¶ĄĮ¢£¬ÓƦĪ±ķŹ¾ÕāĪ»ÓĪæĶÓĪĄĄµÄ¾°µćŹżŗĶƻӊÓĪĄĄµÄ¾°µćŹż²īµÄ¾ų¶ŌÖµ£¬Ēó¦ĪµÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū£®
·ÖĪö£ŗ£Ø1£©ÓĪæĶÓĪĄĄ¾°µćøöŹżĪŖ0£¬1£¬2£¬3£¬¦ĪæÉÄÜȔֵĪŖ£ŗ1£¬3£¬¦Ī=1±ķŹ¾ÓĪĄĄŅ»øö¾°µć»ņÓĪĄĄĮ½øö¾°µć£¬¦Ī=3±ķŹ¾ÓĪĄĄ¾°µćŹżĪŖ0»ņÓĪĄĄĮĖČżøö¾°µć£¬øł¾Żn“Ī¶ĄĮ¢ÖŲø“ŹŌŃéÖŠŹĀ¼ž·¢ÉśkµÄøÅĀŹ¹«Ź½¼“æÉĒóµĆP£Ø¦Ī=1£©£¬P£Ø¦Ī=3£©£¬½ų¶ųµĆµ½·Ö²¼ĮŠŗĶĘŚĶū£»
£Ø2£©µ±n=2k+1£¬k”ŹN*Ź±£¬ÓĪæĶÓĪĄĄ¾°µćøöŹżæÉÄÜĪŖ£ŗ0£¬1£¬2£¬”£¬2k+1£¬Ōņ¦ĪæÉÄÜȔֵĪŖ£ŗ1£¬3£¬5£¬”£¬2k+1£®øł¾Ż¶ĄĮ¢ÖŲø“ŹŌŃéÖŠŹĀ¼žA·¢Éśk“ĪµÄøÅĀŹ¼ĘĖć¹«Ź½Ēó³ö¦ĪČ”ø÷ÖµŹĒµÄøÅĀŹ£¬±ķŹ¾³öE¦Ī=£Ø2k+1-0£©”Į2”Į(
)2k+1
+[£Ø2k+1-1£©-1]”Į2”Į
(
)2k+1+[£Ø2k+1-2£©-2]”Į2”Į
(
)2k+1+”+[2k+1-k£©-k]”Į2”Į
(
)2k+1£¬·Ö×éŗóĄūÓĆŠŌÖŹ
=n
£Øi=1£¬2£¬3£¬”£¬n£©¶ŌÉĻŹ½¼“æɽųŠŠ»Æ¼ņ£¬×īŗóŌŁ»»ĪŖn¼“æÉ£»
£Ø2£©µ±n=2k+1£¬k”ŹN*Ź±£¬ÓĪæĶÓĪĄĄ¾°µćøöŹżæÉÄÜĪŖ£ŗ0£¬1£¬2£¬”£¬2k+1£¬Ōņ¦ĪæÉÄÜȔֵĪŖ£ŗ1£¬3£¬5£¬”£¬2k+1£®øł¾Ż¶ĄĮ¢ÖŲø“ŹŌŃéÖŠŹĀ¼žA·¢Éśk“ĪµÄøÅĀŹ¼ĘĖć¹«Ź½Ēó³ö¦ĪČ”ø÷ÖµŹĒµÄøÅĀŹ£¬±ķŹ¾³öE¦Ī=£Ø2k+1-0£©”Į2”Į(
| 1 |
| 2 |
| C | 0 2k+1 |
| C | 1 2k+1 |
| 1 |
| 2 |
| C | 2 2k+1 |
| 1 |
| 2 |
| C | k 2k+1 |
| 1 |
| 2 |
| iC | i n |
| C | i-1 n-1 |
½ā“š£ŗ½ā£ŗ£Ø1£©ÓĪæĶÓĪĄĄ¾°µćøöŹżĪŖ0£¬1£¬2£¬3£¬¦ĪæÉÄÜȔֵĪŖ£ŗ1£¬3£¬
P£Ø¦Ī=1£©=
(
)2(1-
)+
(
)1(1-
)2=2
(
)3=
£¬
P£Ø¦Ī=3£©=
(
)3+
(
)3=2
(
)3=
£¬
¦ĪµÄ·Ö²¼ĮŠĪŖ£ŗ
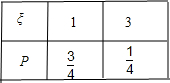
ĖłŅŌE¦Ī=1”Į
+3”Į
=
£®
£Ø2£©µ±n=2k+1£¬k”ŹN*Ź±£¬ÓĪæĶÓĪĄĄ¾°µćøöŹżæÉÄÜĪŖ£ŗ0£¬1£¬2£¬”£¬2k+1£¬
¦ĪæÉÄÜȔֵĪŖ£ŗ1£¬3£¬5£¬”£¬2k+1£®
P£Ø¦Ī=1£©=
(
)k(1-
)k+1+
(
)k+1(1-
)k=2”Į(
)2k+1
£»
P£Ø¦Ī=3£©=
(
)k-1(1-
)k+2+
(
)k+2(1-
)k-1=2”Į(
)2k+1
£»
”
P£Ø¦Ī=2k+1£©=
(
)0(1-
)2k+1+
(
)2k+1(1-
)0=2”Į(
)2k+1
£¬
”ą¦ĪµÄ·Ö²¼ĮŠĪŖ£ŗ

”ąE¦Ī=£Ø2k+1-0£©”Į2”Į(
)2k+1
+[£Ø2k+1-1£©-1]”Į2”Į
(
)2k+1+[£Ø2k+1-2£©-2]”Į2”Į
(
)2k+1+”+[2k+1-k£©-k]”Į2”Į
(
)2k+1
=2”Į(
)2k+1{[£Ø2k+1£©
+2k
+£Ø2k-1£©
+”+£Ø2k+1-k£©
]-[£Ø0”Į
+1
+2”Į
+”+k
]}
=2”Į(
)2k+1{[£Ø2k+1£©”Į
+2k”Į
+£Ø2k-1£©”Į
+”+£Øk+1£©
]-[0”Į
+1”Į
+”+k
]}£¬
ӧ
=n
£Øi=1£¬2£¬3£¬”£¬n£©£¬
E¦Ī=2”Į(
)2k+1{£Ø2k+1£©”Į[
+”
]-£Ø2k+1£©”Į[
+”
]}
=2”Į(
)2k+1”Į£Ø2k+1£©”Į[£Ø
+”
£©-£Ø
+”+
£©]
=2”Į(
)2k+1”Į£Ø2k+1£©”Į
=
£®
“š£ŗ¦ĪµÄŹżŃ§ĘŚĶūE¦ĪĪŖ
£®
P£Ø¦Ī=1£©=
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 3 |
| 1 |
| 2 |
| 3 |
| 4 |
P£Ø¦Ī=3£©=
| C | 3 3 |
| 1 |
| 2 |
| C | 3 3 |
| 1 |
| 2 |
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 4 |
¦ĪµÄ·Ö²¼ĮŠĪŖ£ŗ

ĖłŅŌE¦Ī=1”Į
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
£Ø2£©µ±n=2k+1£¬k”ŹN*Ź±£¬ÓĪæĶÓĪĄĄ¾°µćøöŹżæÉÄÜĪŖ£ŗ0£¬1£¬2£¬”£¬2k+1£¬
¦ĪæÉÄÜȔֵĪŖ£ŗ1£¬3£¬5£¬”£¬2k+1£®
P£Ø¦Ī=1£©=
| C | k 2k+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | k+1 2k+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | k 2k+1 |
P£Ø¦Ī=3£©=
| C | k-1 2k+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | k+2 2k+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | k-1 2k+1 |
”
P£Ø¦Ī=2k+1£©=
| C | 0 2k+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 2k+1 2k+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 0 2k+1 |
”ą¦ĪµÄ·Ö²¼ĮŠĪŖ£ŗ

”ąE¦Ī=£Ø2k+1-0£©”Į2”Į(
| 1 |
| 2 |
| C | 0 2k+1 |
| C | 1 2k+1 |
| 1 |
| 2 |
| C | 2 2k+1 |
| 1 |
| 2 |
| C | k 2k+1 |
| 1 |
| 2 |
=2”Į(
| 1 |
| 2 |
| C | 0 2k+1 |
| C | 1 2k+1 |
| C | 2 2k+1 |
| C | k 2k+1 |
| C | 0 2k+1 |
| ”ĮC | 1 2k+1 |
| C | 2 2k+1 |
| •C | k 2k+1 |
=2”Į(
| 1 |
| 2 |
| C | 2k+1 2k+1 |
| C | 2k 2k+1 |
| C | 2k-1 2k+1 |
| ”ĮC | k+1 2k+1 |
| C | 0 2k+1 |
| C | 1 2k+1 |
| •C | k 2k+1 |
ӧ
| iC | i n |
| C | i-1 n-1 |
E¦Ī=2”Į(
| 1 |
| 2 |
| C | 2k 2k |
| +C | 2k-1 2k |
| +C | k 2k |
| C | 0 2k |
| +C | 1 2k |
| +C | k-1 2k |
=2”Į(
| 1 |
| 2 |
| C | 2k 2k |
| +C | 2k-1 2k |
| +C | k 2k |
| C | 0 2k |
| +C | 1 2k |
| C | k-1 2k |
=2”Į(
| 1 |
| 2 |
| C | k 2k |
=
|
n-1 |
“š£ŗ¦ĪµÄŹżŃ§ĘŚĶūE¦ĪĪŖ
|
n-1 |
µćĘĄ£ŗ±¾Ģāæ¼²éĄėÉ¢ŠĶĖ껜±äĮæµÄ·Ö²¼ĮŠ”¢ĘŚĶū£¬æ¼²én“Ī¶ĄĮ¢ÖŲø“ŹŌŃéÖŠŹĀ¼žA·¢ÉśkµÄøÅĀŹ¼ĘĖć¹«Ź½£¬æ¼²é×éŗĻŹżŠŌÖŹÓ¦ÓĆ£¬æ¼²éѧɜ×ŪŗĻŌĖÓĆÖŖŹ¶·ÖĪö½ā¾öĪŹĢāµÄÄÜĮ¦£¬±¾Ģā×ŪŗĻŠŌĒ棬ÄÜĮ¦ŅŖĒóøߣ¬ŹōÄŃĢā£®

Į·Ļ°²įĻµĮŠ“š°ø
 Ķ¬²½°ĀŹżĻµĮŠ“š°ø
Ķ¬²½°ĀŹżĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ