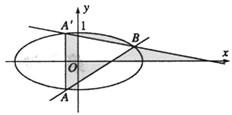
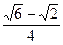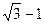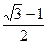题目内容
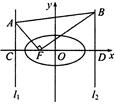
(本小题满分18分)过直线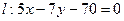 上的点
上的点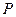 作椭圆
作椭圆 的切线
的切线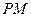 、
、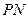 ,切点分别为
,切点分别为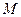 、
、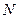 ,联结
,联结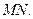 (1)当点
(1)当点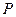 在直线
在直线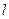 上运动时,证明:直线
上运动时,证明:直线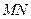 恒过定点
恒过定点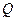 ;
;
(2)当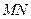 ∥
∥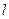 时,定点
时,定点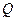 平分线段
平分线段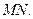
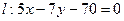 上的点
上的点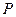 作椭圆
作椭圆 的切线
的切线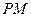 、
、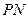 ,切点分别为
,切点分别为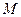 、
、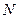 ,联结
,联结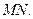 (1)当点
(1)当点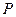 在直线
在直线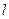 上运动时,证明:直线
上运动时,证明:直线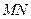 恒过定点
恒过定点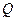 ;
;(2)当
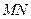 ∥
∥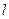 时,定点
时,定点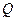 平分线段
平分线段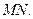
(1)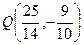 (2)略
(2)略
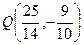 (2)略
(2)略:设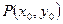 、
、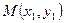 、
、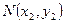 . 则椭圆过点
. 则椭圆过点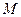 、
、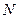 的切线方程分别为
的切线方程分别为
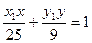 ,
,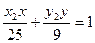 (3分)因为两切线都过点
(3分)因为两切线都过点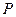 ,则有
,则有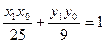 ,
,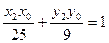 .这表明
.这表明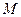 、
、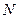 均在直线
均在直线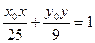 ①上.由两点决定一条直线知,式①就是直线
①上.由两点决定一条直线知,式①就是直线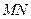 的方程,其中
的方程,其中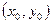 满足直线
满足直线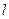 的方程.………(6分)
的方程.………(6分)
(1)当点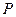 在直线
在直线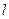 上运动时,可理解为
上运动时,可理解为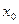 取遍一切实数,相应的
取遍一切实数,相应的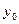 为
为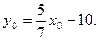
代入①消去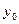 得
得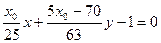 ②对一切
②对一切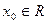 恒成立.……(9分)
恒成立.……(9分)
变形可得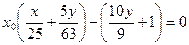 对一切
对一切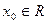 恒成立.故有
恒成立.故有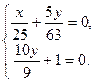 由此解得直线
由此解得直线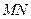 恒过定点
恒过定点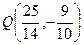 .(12分)
.(12分)
(2)当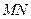 ∥
∥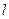 时,由式②知
时,由式②知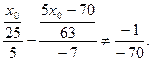 解得
解得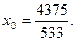
代入②,得此时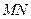 的方程为
的方程为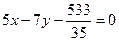 ③
③
将此方程与椭圆方程联立,消去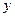 得
得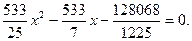 ……(15分)
……(15分)
由此可得,此时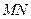 截椭圆所得弦的中点横坐标恰好为点
截椭圆所得弦的中点横坐标恰好为点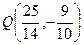 的横坐标,即
的横坐标,即
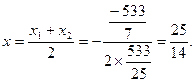 代入③式可得弦中点纵坐标恰好为点
代入③式可得弦中点纵坐标恰好为点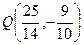 的纵坐标,即
的纵坐标,即
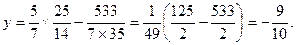 这就是说,点
这就是说,点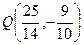 平分线段
平分线段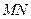 .……(18分)
.……(18分)
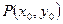 、
、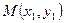 、
、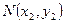 . 则椭圆过点
. 则椭圆过点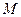 、
、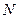 的切线方程分别为
的切线方程分别为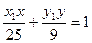 ,
,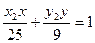 (3分)因为两切线都过点
(3分)因为两切线都过点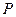 ,则有
,则有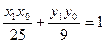 ,
,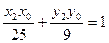 .这表明
.这表明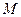 、
、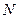 均在直线
均在直线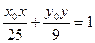 ①上.由两点决定一条直线知,式①就是直线
①上.由两点决定一条直线知,式①就是直线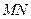 的方程,其中
的方程,其中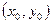 满足直线
满足直线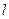 的方程.………(6分)
的方程.………(6分)(1)当点
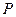 在直线
在直线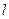 上运动时,可理解为
上运动时,可理解为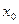 取遍一切实数,相应的
取遍一切实数,相应的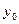 为
为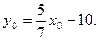
代入①消去
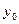 得
得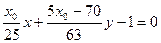 ②对一切
②对一切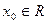 恒成立.……(9分)
恒成立.……(9分)变形可得
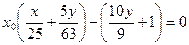 对一切
对一切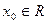 恒成立.故有
恒成立.故有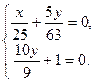 由此解得直线
由此解得直线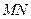 恒过定点
恒过定点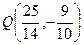 .(12分)
.(12分)(2)当
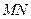 ∥
∥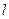 时,由式②知
时,由式②知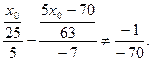 解得
解得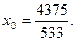
代入②,得此时
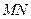 的方程为
的方程为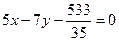 ③
③将此方程与椭圆方程联立,消去
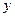 得
得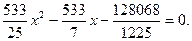 ……(15分)
……(15分)由此可得,此时
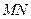 截椭圆所得弦的中点横坐标恰好为点
截椭圆所得弦的中点横坐标恰好为点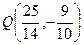 的横坐标,即
的横坐标,即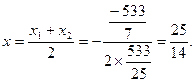 代入③式可得弦中点纵坐标恰好为点
代入③式可得弦中点纵坐标恰好为点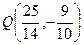 的纵坐标,即
的纵坐标,即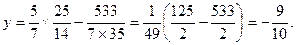 这就是说,点
这就是说,点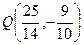 平分线段
平分线段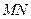 .……(18分)
.……(18分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
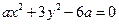 的一个焦点坐标为
的一个焦点坐标为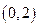 ,求
,求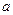 的值。
的值。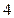 ,与圆柱底面成
,与圆柱底面成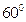 角的平面截这个圆柱得到一个椭圆,则这个椭圆的离心率为 。
角的平面截这个圆柱得到一个椭圆,则这个椭圆的离心率为 。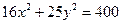 的长轴长和短轴长、离心率、焦点和顶点坐标及准线方程。
的长轴长和短轴长、离心率、焦点和顶点坐标及准线方程。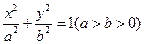 与直线
与直线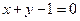 相交于
相交于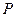 、
、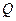 两点,且
两点,且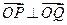 (
(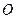 为坐标原点).(Ⅰ)求证:
为坐标原点).(Ⅰ)求证: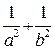 等于定值;
等于定值;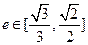 时,求椭圆长轴长的取值范围.
时,求椭圆长轴长的取值范围.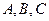 均在椭圆
均在椭圆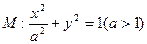 上,直线
上,直线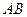 、
、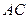 分别过椭圆的左右焦点
分别过椭圆的左右焦点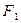 、
、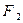 ,当
,当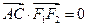 时,有
时,有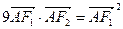 .
.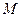 的方程;
的方程;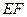 为圆
为圆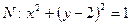 的任一条直径,求
的任一条直径,求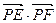 的最大值.
的最大值.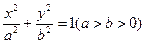 的左、右准线分别为
的左、右准线分别为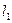 、
、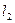 ,且分别交
,且分别交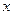 轴于
轴于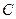 、
、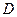 两点,从
两点,从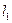 上一点
上一点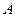 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点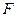 被
被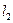 交于点
交于点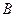 ,若
,若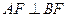 ,且
,且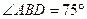 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )