题目内容
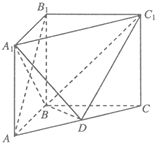 (2013•唐山二模)如图,直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,∠ABC=90°,D是AC的中点.
(2013•唐山二模)如图,直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,∠ABC=90°,D是AC的中点.(Ⅰ)求证:AB1∥平面BC1D;
(Ⅱ)求几何体BDA1B1C1的体积.
分析:(I)连接B1C,交BC1于点P,连接PD.由平行四边形的性质,得到PD是△AB1C的中位线,得PD∥B1A,结合线面平行的判定定理,证出AB1∥平面BC1D;
(II)根据题中数据,算出直三棱柱ABC-A1B1C1的体积V1=S△ABC×CC1=4.由三棱锥C1-BDC与三棱锥A1-BDA的底面积相等,且高也相等可得它们的体积都等于
×
×V1=
.最后用直三棱柱ABC-A1B1C1的体积,减去三棱锥C1-BDC与三棱锥A1-BDA的体积之和,即可得到几何体BDA1B1C1的体积.
(II)根据题中数据,算出直三棱柱ABC-A1B1C1的体积V1=S△ABC×CC1=4.由三棱锥C1-BDC与三棱锥A1-BDA的底面积相等,且高也相等可得它们的体积都等于
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
解答: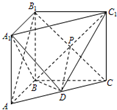 解:(Ⅰ)连接B1C,交BC1于点P,连接PD.
解:(Ⅰ)连接B1C,交BC1于点P,连接PD.
∵BB1C1C是平行四边形,∴B1C与BC1互相平分,可得P为为B1C的中点
∵D为AC的中点,∴PD是△AB1C的中位线,得PD∥B1A,
又∵PD?平面B1CD,B1A?平面BC1D,
∴AB1∥平面BC1D.…(6分)
(Ⅱ)∵△ABC中,∠ABC=90°,AB=BC=2
∴△ABC的面积为S△ABC=
×2×2=2
由此可得:直三棱柱ABC-A1B1C1的体积V1=S△ABC×CC1=2×2=4.
∵三棱锥C1-BDC与三棱锥A1-BDA的底面积相等,且高也相等
∴三棱锥C1-BDC的体积V2与三棱锥A1-BDA的体积V3相等,
可得V2=V3=
×
V1=
.
因此,几何体BDA1B1C1的体积V=V1-V2-V3=4--
-
=
.…(12分)
 解:(Ⅰ)连接B1C,交BC1于点P,连接PD.
解:(Ⅰ)连接B1C,交BC1于点P,连接PD.∵BB1C1C是平行四边形,∴B1C与BC1互相平分,可得P为为B1C的中点
∵D为AC的中点,∴PD是△AB1C的中位线,得PD∥B1A,
又∵PD?平面B1CD,B1A?平面BC1D,
∴AB1∥平面BC1D.…(6分)
(Ⅱ)∵△ABC中,∠ABC=90°,AB=BC=2
∴△ABC的面积为S△ABC=
| 1 |
| 2 |
由此可得:直三棱柱ABC-A1B1C1的体积V1=S△ABC×CC1=2×2=4.
∵三棱锥C1-BDC与三棱锥A1-BDA的底面积相等,且高也相等
∴三棱锥C1-BDC的体积V2与三棱锥A1-BDA的体积V3相等,
可得V2=V3=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
因此,几何体BDA1B1C1的体积V=V1-V2-V3=4--
| 2 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
点评:本题在直三棱柱中求证线面平行并求特殊多面体的体积,着重考查了线面平行的判定定理和柱体、锥体体积的计算等知识,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目