题目内容
若一个底面是正三角形的三棱柱的主视图如右图所示，其顶点都在一个球面上，则该球的表面积（ ）分析：由已知的正视图，可得该三棱柱的底面棱长和高，进而求出底面外接圆半径r及球半径R，最后依据球的表面积公式求出球的表面积．
解答：解：由已知底面是正三角形的三棱柱的正视图，
可得该三棱柱的底面棱长为2，高为1．
则底面外接圆半径r=
，球心到底面的球心距d=
∴球半径R2=
+
=
∴该球的表面积S=4πR2=
π
故选C．
可得该三棱柱的底面棱长为2，高为1．
则底面外接圆半径r=
2
| ||
| 3 |
| 1 |
| 2 |
∴球半径R2=
| 4 |
| 3 |
| 1 |
| 4 |
| 19 |
| 12 |
∴该球的表面积S=4πR2=
| 19 |
| 3 |
故选C．
点评：本题考查的知识点是由三视图求表面积、球的表面积等基础知识，考查运算求解能力与转化思想．属于基础题．
练习册系列答案
相关题目
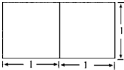若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
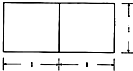若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为
（2013•肇庆一模）若一个底面是正三角形的三棱柱的正视图如图所示，则其表面积等于