题目内容
(必修3做)甲、乙两人玩数字游戏的规则如下:甲、乙两人都从集合{1,2,3,4}中任选一个数写在纸上,并分别记为a、b,若|a-b|≤1,则称甲、乙两人“心有灵犀”,那么甲、乙两人在一次游戏中“心有灵犀”的概率为
- A.

- B.

- C.

- D.

C
分析:甲、乙两人所有的选数方法共有4×4=16 种,满足|a-b|≤1的方法数为 2×3+4=10,从而得到所求事件的
概率为 =
= .
.
解答:甲、乙两人都从集合{1,2,3,4}中任选一个数写在纸上的方法总数为 4×4=16,
满足|a-b|≤1的方法数为 2×3+4=10.
故甲、乙两人在一次游戏中“心有灵犀”的概率为 =
= ,
,
故选C.
点评:本题考查等可能事件的概率,求出满足|a-b|≤1的方法数为 2×3+4=10,是解题的关键.
分析:甲、乙两人所有的选数方法共有4×4=16 种,满足|a-b|≤1的方法数为 2×3+4=10,从而得到所求事件的
概率为
 =
= .
.解答:甲、乙两人都从集合{1,2,3,4}中任选一个数写在纸上的方法总数为 4×4=16,
满足|a-b|≤1的方法数为 2×3+4=10.
故甲、乙两人在一次游戏中“心有灵犀”的概率为
 =
= ,
,故选C.
点评:本题考查等可能事件的概率,求出满足|a-b|≤1的方法数为 2×3+4=10,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
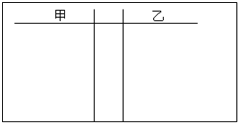 (必修3做) 在2008年奥运会上甲、乙两名射击运动员在比赛中打出如下成绩:
(必修3做) 在2008年奥运会上甲、乙两名射击运动员在比赛中打出如下成绩:


