题目内容

讨论函数在[-1，1]上的单调性．
解：设x1、x2∈[-1，1]且x1＜x2，即-1≤x1＜x2≤1，
则，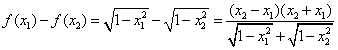
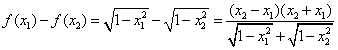当1＞x1≥0，1≥x2＞0，x1＜x2时，f(x1)＞f(x2)，
∴f(x)在[0，1]上为减函数；
当-1≤x1＜0，-1＜x2≤0，x1＜x2时，f(x1)＜f(x2)，
∴f(x)在[-1，0]上为增函数．
练习册系列答案
相关题目
设函数f（x）=xekx（k≠0），
（1）求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）讨论函数f（x）的单调性；
（3）设g（x）=x2-2bx+4，当k=1时，若对任意x1∈R，存在x2∈[1，2]，使f（x1）≥g（x2），求实数b取值范围．
（2013•黄冈模拟）已知函数f（x）=ax3+x2-ax （a∈R且a≠0）．
（I）若函数f（x）在{-∞，-1）和（
1
3
，+∞）上是增函数在（-1
1
3
）上 是减函数，求a的值；
（II）讨论函数g（x）=
f(x)
x
-
3
a
lnx的单调递减区间；
（III）如果存在a∈（-∞，-1），使函数h（x）=f（x）+f′（x），x∈[-1，b]（b＞-1），在x=-1处取得最小值，试求b的最大值．
（2012•钟祥市模拟）已知函数f（x）=lnx-ax2+（a-2）x．
（I）讨论函数f（x）的单调性；
（II）若f（x）在点（1，f（1））处的切线斜率为-2．
（i）求f（x）的解析式；
（ii）求证：当x＞0且x≠1时，
f(x)
x+1
+x+
1
x
＞
lnx
x-1
．
已知函数f（x）=ax-1-lnx（a∈R）
①当a=
12
时，求函数在[1，e]上的最大值和最小值；
②讨论函数的单调性；
③若函数f（x）在x=1处取得极值，不等式f（x）≥bx-2对?x∈（0，+∞）恒成立，求实数b的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网