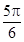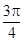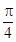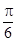题目内容
已知函数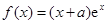 ,其中
,其中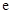 是自然对数的底数,
是自然对数的底数,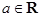 .
.
(Ⅰ)求函数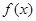 的单调区间;
的单调区间;
(Ⅱ)当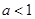 时,试确定函数
时,试确定函数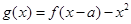 的零点个数,并说明理由.
的零点个数,并说明理由.
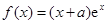 ,其中
,其中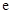 是自然对数的底数,
是自然对数的底数,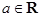 .
.(Ⅰ)求函数
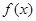 的单调区间;
的单调区间;(Ⅱ)当
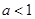 时,试确定函数
时,试确定函数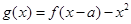 的零点个数,并说明理由.
的零点个数,并说明理由.(Ⅰ)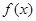 的单调减区间为
的单调减区间为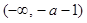 ;单调增区间为
;单调增区间为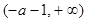 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
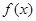 的单调减区间为
的单调减区间为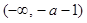 ;单调增区间为
;单调增区间为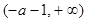 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)求导得,
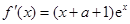 ,因为
,因为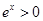 ,所以
,所以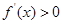 的解集为
的解集为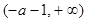 ,即单调递增区间;
,即单调递增区间;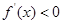 的解集为
的解集为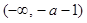 ,即单调递减区间;(Ⅱ)函数
,即单调递减区间;(Ⅱ)函数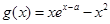 ,令
,令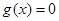 ,得
,得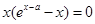 ,显然
,显然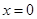 是一个零点,记
是一个零点,记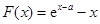 ,求导得
,求导得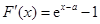 ,易知
,易知 时
时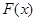 递减;
递减;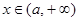 时
时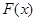 递增,故
递增,故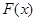 的最小值
的最小值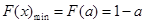 ,又
,又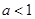 ,故
,故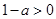 ,即
,即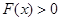 ,所以函数
,所以函数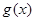 的零点个数1个.
的零点个数1个.试题解析:(Ⅰ)解:因为
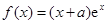 ,
,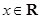 ,所以
,所以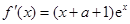 .
.令
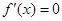 ,得
,得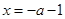 .当
.当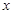 变化时,
变化时,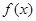 和
和 的变化情况如下:
的变化情况如下: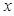 | 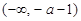 | 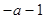 | 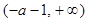 |
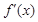 | 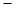 |  |  |
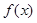 | ↘ | | ↗ |
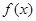 的单调减区间为
的单调减区间为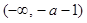 ;单调增区间为
;单调增区间为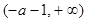 .
.(Ⅱ)解:结论:函数
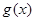 有且仅有一个零点. 理由如下:
有且仅有一个零点. 理由如下:由
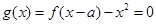 ,得方程
,得方程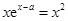 , 显然
, 显然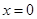 为此方程的一个实数解.
为此方程的一个实数解. 所以
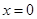 是函数
是函数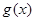 的一个零点. 当
的一个零点. 当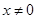 时,方程可化简为
时,方程可化简为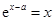 .设函数
.设函数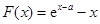 ,则
,则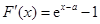 ,令
,令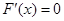 ,得
,得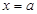 .
.当
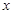 变化时,
变化时,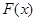 和
和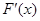 的变化情况如下:
的变化情况如下: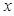 | 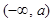 | 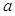 | 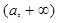 |
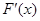 | 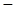 | 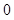 | 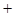 |
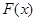 | ↘ | | ↗ |
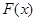 的单调增区间为
的单调增区间为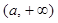 ;单调减区间为
;单调减区间为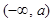 .所以
.所以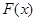 的最小值
的最小值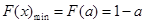 .
. 因为
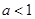 ,所以
,所以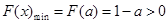 ,所以对于任意
,所以对于任意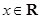 ,
,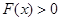 ,因此方程
,因此方程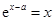 无实数解.所以当
无实数解.所以当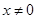 时,函数
时,函数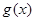 不存在零点.综上,函数
不存在零点.综上,函数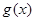 有且仅有一个零点. 考点:
有且仅有一个零点. 考点:
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
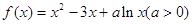 .
.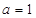 ,求函数
,求函数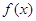 的单调区间和极值;
的单调区间和极值;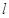 的斜率为
的斜率为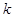 ,当
,当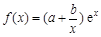 .
.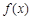 在(0,+∞)内的极值;
在(0,+∞)内的极值;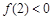 ,
,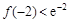 ,且
,且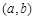 形成的平面区域的面积.
形成的平面区域的面积.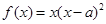 ,
,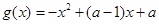 (其中
(其中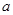 为常数);
为常数);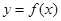 和
和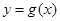 有相同的极值点,求
有相同的极值点,求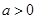 ,问是否存在
,问是否存在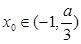 ,使得
,使得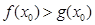 ,若存在,请求出实数
,若存在,请求出实数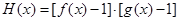 ,若函数
,若函数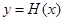 有5个不同的零点,求实数
有5个不同的零点,求实数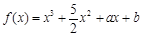 (
(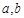 为常数),其图象是曲线
为常数),其图象是曲线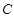 .
.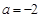 时,求函数
时,求函数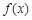 的单调减区间;
的单调减区间;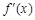 ,若存在唯一的实数
,若存在唯一的实数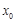 ,使得
,使得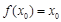 与
与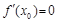 同时成立,求实数
同时成立,求实数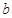 的取值范围;
的取值范围;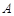 为曲线
为曲线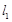 与曲线
与曲线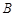 ,在点
,在点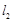 ,设切线
,设切线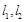 的斜率分别为
的斜率分别为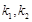 .问:是否存在常数
.问:是否存在常数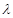 ,使得
,使得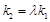 ?若存在,求出
?若存在,求出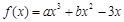
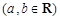 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.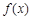 的解析式;
的解析式;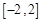 上任意两个自变量的值
上任意两个自变量的值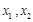 ,都有
,都有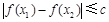 ,求实数
,求实数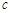 的最小值;
的最小值;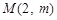
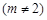 ,可作曲线
,可作曲线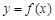 的三条切线,求实数
的三条切线,求实数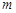 的取值范围.
的取值范围.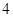 元,并且每件商品需向总店交
元,并且每件商品需向总店交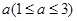 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为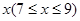 元时,一年的销售量为
元时,一年的销售量为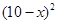 万件.
万件.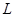 (万元)与每件商品的售价
(万元)与每件商品的售价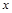 的函数关系式
的函数关系式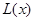 ;
;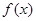 满足:
满足: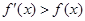 恒成立,若
恒成立,若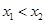 ,则
,则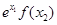 与
与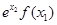 的大小关系为 ( )
的大小关系为 ( )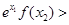
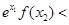
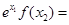
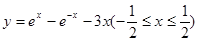 图象上任意一点,且在点P处切线的倾斜角为
图象上任意一点,且在点P处切线的倾斜角为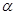 ,则
,则