题目内容
设变量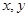
满足约束条件
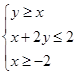，则
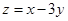的最小值为（ ）
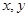满足约束条件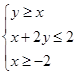，则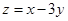的最小值为（ ）A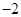． | B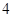． | C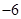． | D． |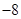
D
试题分析：根据已知条件可知，设变量
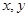满足约束条件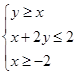，那么可知不等式的表示的区域为围成了三角形区域，区域的边界点为（-2，2）（-2，-2）（
），那么可知当目标函数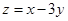在平移中过点（-2，2）时，截距最大，目标函数最小，故为-8，故选D.点评：解决该试题的关键是能利用不等式组表示的平面区域，结合目标函数平移，当截距最大时，其过的点为最优解点，也就是目标函数取得最小值,属于基础题。
练习册系列答案
阅读快车系列答案
相关题目
，则目标函数
的最大值为 ．
满足
则点
到直线
，
及直线
的距离之和的最大值是 ；
满足：
，则
的最大值是（ ）
满足
，设
，则
的取值范围是( )．
，
]
为常数
表示的平面区域的面积为8，则
的最小值为（ ）
满足不等式组
,且
的最小值为
,则实数
的值是 ．
满足约束条件
则
的最小值为（ ）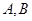
两型会议桌，每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套