题目内容
9.如图1,已知在矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使平面ADE⊥平面ABCE,如图2,F是DE的中点,H是AB上的一点,满足AH=3HB.(1)求证:FH∥平面DBC;
(2)求二面角B-CE-D的正弦值.

分析 (1)取EC的中点G,根据面面平行的性质定理证明平面FGH∥平面DBC,即可证明FH∥平面DBC;
(2)建立空间直角坐标系,求出平面的法向量,利用向量法即可求二面角B-CE-D的正弦值.
解答 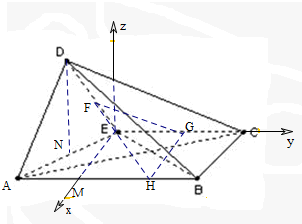 证明:(1)取AB的中点M,EC的中点G,连接FG,FH,GH,
证明:(1)取AB的中点M,EC的中点G,连接FG,FH,GH,
∵AH=3HB.
∴H是BM的中点,
∵F是DE的中点,
∴FG∥DC,GH∥BC,
∵DC∩BC=C,
∴平面FGH∥平面DBC,
由FH?平面FGH,
∴FH∥平面DBC;
(2)取AE的中点N,连接DN,
∵平面ADE⊥平面ABCE,△ADE是等腰三角形,
∴DN⊥AE,
以E为坐标原点,以EA,EC,分别为x,y轴,建立空间直角坐标系如图,
则B(2,2,0),C(0,2,0),E(0,0,0),A(2,-2,0),N(1,-1,0),D(1,-1,$\sqrt{2}$),
则平面BCE的一个法向量为$\overrightarrow{m}$=(0,0,1),
设平面CED的法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{EC}$=(0,2,0),$\overrightarrow{ED}$=(1,-1,$\sqrt{2}$),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EC}=0}\\{\overrightarrow{n}•\overrightarrow{ED}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2y=0}\\{x-y+\sqrt{2}z=0}\end{array}\right.$,
令z=1,则y=0,x=-$\sqrt{2}$,
即$\overrightarrow{n}$=(=-$\sqrt{2}$,0,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{1×\sqrt{(-\sqrt{2})^{2}+1}}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
则sin<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\sqrt{1-(\frac{\sqrt{3}}{3})^{2}}$=$\sqrt{1-\frac{1}{3}}=\sqrt{\frac{2}{3}}$=$\frac{\sqrt{6}}{3}$
即二面角B-CE-D的正弦值为$\frac{\sqrt{6}}{3}$.
点评 本小题主要考查直线与平面垂直的性质,以及几二面角的度量等基础知识,考查利用空间向量的方程解决问题的能力,化归与转化思想,属于中档题.

 名校课堂系列答案
名校课堂系列答案| 甲平均成绩 | 83 | 91 | 80 | 79 | 92 | 85 |
| 乙平均成绩 | 92 | 93 | 80 | 84 | 82 | 79 |
(Ⅰ)现要选派一个实验班参加测试团体赛,从统计学角度,你认为选派哪个实验班合理?说明理由;
(Ⅱ)对选派的实验班在团体赛的三次比赛成绩进行预测,记这三次平均成绩中不低于85分的次数为X,求X的分布列及数学期望EX.
| A. | a=0,b=0 | B. | a=1,b=0 | C. | a=0,b=1 | D. | a=0,b∈R |