题目内容
已知椭圆
+
=1，能否在椭圆上位于y轴左侧部分上找到一点M，使点M到左准线l的距离|MN|为点M到两焦点F1、F2的距离的等比中项？并说明理由.
思路解析：运用椭圆的两个定义及等比中项的定义沟通已知与未知之间的联系. 解：由已知，a=2,b= 方法归纳 本题为“探索型”命题，一般解题思路是假设M满足条件，由此得到合理（或不合理）的结果，从而判断M存在或不存在，这便是说明理由或证明过程.
,c=1,e=,左准线l的方程为x=-4，设椭圆上位于y轴左侧部分存在点M(x0,y0)(-2≤x0＜0
，满足|MN|2=|MF1|·|MF2|①，由椭圆的焦半径公式为|MF1|=a+ex0=2+
x0,|MF2|=a-ex0=2-
x0,又|MN|=|MF1|·
=2|MF1|=4+x0,将以上各式代入①中,得(4+x0)=(2+
x0)(2-
x0)2,整理得5x0+32x0+48=0,解得x0=-2.4或x0=-4，这与-2≤x0＜0相矛盾，所以这样的点M不存在.
练习册系列答案
完美读法系列答案
美文赏读系列答案
必考点灵通复习法系列答案
名校调研系列卷每周一考系列答案
同步解析与测评初中总复习指导与训练系列答案
专题分类卷系列答案
英语组合阅读系列答案
学习指导用书系列答案
精讲精练宁夏人民教育出版社系列答案
课课练强化练习系列答案
相关题目
已知椭圆C的方程是
+
=1（0＜b＜2）的左焦点为F，左、右顶点分别为A、C，上顶点为B，过F、B、C作圆P．
时，求圆P的方程；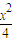
+
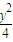=1（0＜b＜2）的左焦点为F，左、右顶点分别为A、C，上顶点为B，过F、B、C作圆P．
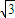时，求圆P的方程；
+
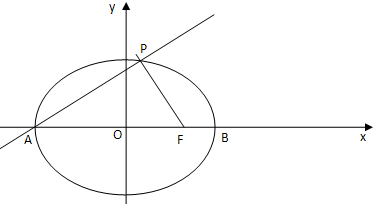
=1（a＞b＞0）的长轴长为4，离心率为
，点P是椭圆上异于顶点的任意一点，过点P作椭圆的切线l，交y轴于点A，直线l′过点P且垂直于l，交y轴于点B、