题目内容

【题目】已知双曲线的左、右焦点分别为、，是双曲线上一点，且轴，若的内切圆半径为，则其渐近线方程是__________．

【答案】

【解析】分析：由题意可得A在双曲线的右支上，由双曲线的定义可得|AF1|﹣|AF2|=2a，设Rt△AF1F2内切圆半径为r，运用等积法和勾股定理，可得r=c﹣a，结合条件和渐近线方程，计算即可得到所求．

详解：由点A在双曲线上，且AF2⊥x轴，

可得A在双曲线的右支上，

由双曲线的定义可得|AF1|﹣|AF2|=2a，

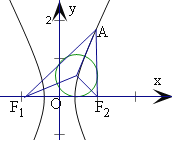
设Rt△AF1F2内切圆半径为r，

运用面积相等可得S=|AF2||F1F2|

=r（|AF1|+|AF2|+|F1F2|），

由勾股定理可得|AF2|2+|F1F2|2=|AF1|2，

解得r=，

，即

∴渐近线方程是，

故答案为：．

练习册系列答案
相关题目

【题目】已知函数.

（1）当时，求在区间上的最值；

（2）讨论函数的单调性；

（3）当时，有恒成立，求的取值范围.

【题目】设f（x）=|x﹣3|+|x﹣4|．
（1）求函数 的定义域；
（2）若存在实数x满足f（x）≤ax﹣1，试求实数a的取值范围．

【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏，但可见部分如下，据此解答如下问题：

（Ⅰ）求分数在[50，60）的频率及全班人数；
（Ⅱ）求分数在[80，90）之间的频数，并计算频率分布直方图中[80，90）间的矩形的高；
（Ⅲ）若规定：75（包含75分）分以上为良好，90分（包含90分）以上为优秀，要从分数在良好以上的试卷中任取两份分析学生失分情况，设在抽取的试卷中，分数为优秀的试卷份数为X，求X的概率分布列及数学期望．

【题目】设抛物线C：x2=4y的焦点为F，斜率为k的直线l经过点F，若抛物线C上存在四个点到直线l的距离为2，则k的取值范围是（ ）
A.（﹣∞，﹣ ）∪（ ，+∞）
B.（﹣ ，﹣1）∪（1， ）
C.（﹣ ， ）
D.（﹣∞，﹣1）∪（1，+∞）

【题目】如图，在四边形中，，，四边形为矩形，且平面，.

（1）求证：平面；

（2）点在线段上运动，当点在什么位置时，平面与平面所成锐二面角最大，并求此时二面角的余弦值.

【题目】正四棱柱中，，则与平面所成角的正弦值为__________．

【题目】已知函数．

（1）当a=3时，方程的解的个数；

（2）对任意时，函数的图象恒在函数图象的下方，求a的取值范围；

（3）在上单调递增，求a的范围；

【题目】若函数f（x）=x3+ax2+bx（a，b∈R）的图象与x轴相切于一点A（m，0）（m≠0），且f（x）的极大值为 ，则m的值为（ ）
A.
B.
C.
D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网