题目内容
(08年湖北卷理)(本小题满分14分)
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数.
其中λ为实数,n为正整数.
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有
a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
(1)证明;假设存在一个实数![]() ,使
,使![]() 是等比数列,则有
是等比数列,则有![]() ,
,
即![]() 矛盾。
矛盾。
所以![]() 不是等比数列。
不是等比数列。
(2)解:因为
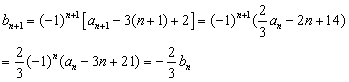
又![]() ,所以
,所以
当![]() 时,
时,![]() 些时
些时![]() 不是等比数列;
不是等比数列;
当![]() 时,
时,![]() 由上可知
由上可知![]() 。
。
故当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列。
为公比的等比数列。
(3)由(2)知,当![]() 时,
时,![]() 不满足题目要求。
不满足题目要求。
![]() ,故得
,故得![]() 可得
可得
![]() 。
。
要使![]() 对任意正整数
对任意正整数![]() 成立
成立
即![]()
得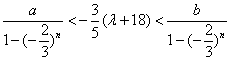 ......①
......①
令![]() ,则
,则
当![]() 为正奇数时,
为正奇数时,![]() ;当
;当![]() 为正偶数时,
为正偶数时,![]() .
.
所以![]() 的最大值为
的最大值为![]() ,
,![]() 的最小值为
的最小值为![]() ,
,
于是,由式①得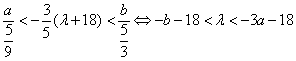 .
.
当![]() 时,由
时,由![]() 知,不存在实数
知,不存在实数![]() 满足题目要求;
满足题目要求;
当时![]() ,存在实数
,存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ,且
,且![]() 的取值范围是
的取值范围是![]() 。
。
【试题解析】第(1)问问的是证明![]() “不是等比数列”,这样的问题显然用“反证法”;第(2)正着问,那就顺着推;第(3)问要先求和再解建立不等式。
“不是等比数列”,这样的问题显然用“反证法”;第(2)正着问,那就顺着推;第(3)问要先求和再解建立不等式。
【高考考点】本题主要考查等比数列的定义、数列求和、不等式基础知识和分类讨论的思想,考查综合分析问题的能力和推理能力。
【易错提醒】本题主要是,没有掌握解题的基本方法,再就是没有分类讨论。
【备考提示】对等比数列、等差数列、数求和的知识要熟练掌握,数列中要特别注意递推关系式的结构。

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目



