Question

【题目】已知圆，点是直线上的一动点，过点作圆的切线，切点为.

(1)当切线的长度为时，求线段PM长度.

(2)若的外接圆为圆，试问：当在直线上运动时，圆是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由；

(3)求线段长度的最小值．

Answer 1

【答案】（1）8（2）（3）

【解析】试题分析：（1）根据圆中切线长的性质得到；（2）设，经过A,P,M三点的圆N以MP为直径，圆N的方程为化简求值即可；（3）（Ⅲ）求出点M到直线AB的距离，利用勾股定理，即可求线段AB长度的最小值.

解析：

（1）由题意知，圆M的半径r=4，圆心M(0，6)，设

PA是圆的一条切线，

(2)设， 经过A,P,M三点的圆N以MP为直径，

圆心，半径为

得圆N的方程为

即，有

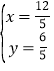
由，解得或 圆过定点

(3) 圆N的方程，即 ①

圆 即 ②

②-①得：圆M与圆N相交弦AB所在直线方程为：

圆心M(0,6)到直线AB的距离

弦长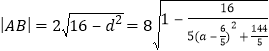

当时，线段AB长度有最小值.