题目内容
设函数 定义在
定义在 上,对于任意实数
上,对于任意实数 ,恒有
,恒有
 ,且当
,且当 时,
时,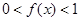
(1)求证:
 且当
且当 时,
时,
(2)求证:
 在
在 上是减函数;
上是减函数;
(3)设集合 ,
, ,且
,且 ,
,
求实数 的取值范围。
的取值范围。
【答案】
(1)见解析;(2)见解析;(3)
【解析】(Ⅰ)在证明f(0)=1及x<0,f(x)>1时,要注意利用f(m+n)=f(m)f(n),根据题目的要求,灵活赋值求证。(II)要注意利用定义。(3)根据前两问的结论,可知 ,抛物线
,抛物线 与直线y=a没有交点求实数a的范围。进而转化为求二次函数的最值问题。
与直线y=a没有交点求实数a的范围。进而转化为求二次函数的最值问题。
(1)证明: ,
, 为任意实数,
为任意实数,
取 ,则有
,则有
 当
当 时,
时, ,
, ,
,
 ……1分
……1分
当 时,
时,
 ,则
,则
取  则
则
则
 ……4分
……4分
(2)证明:由(1)及题设可知,在 上
上
 ,
,


 …………6分
…………6分


所以 在
在 上是减函数…………9分
上是减函数…………9分
(3)解:在集合 中
中
由已知条件,有
 ,即
,即 ………11分
………11分
在集合 中,有
中,有

 ,则抛物线
,则抛物线 与直线
与直线 无交点
无交点

 ,
, ,
,
即 的取值范围是
的取值范围是 …………14分
…………14分

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
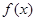 是定义在
是定义在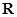 上的增函数,且对于任意的
上的增函数,且对于任意的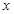 都有
都有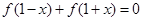 恒成立. 如果实数
恒成立. 如果实数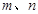 满足不等式组
满足不等式组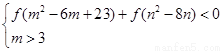 ,那么
,那么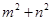 的取值范围是
的取值范围是 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则 是
是 ,若
,若  +
+
 ,
,