题目内容
已知抛物线y2=-x与直线y=k(x+1)相交于A、B两点.(1)求证:OA⊥OB;
(2)当△OAB的面积等于![]() 时,求k的值.
时,求k的值.
(1)证明:如下图,由方程组 消去x,并整理得ky2+y-k=0.
消去x,并整理得ky2+y-k=0.

设A(x1,y1),B(x2,y2),由韦达定理y1·y2=-1.
∵A、B在抛物线y2=-x上,
∴y12=-x1,y22=-x2,y12·y22=x1x2.
∵kOA·kOB=![]() =-1,
=-1,
∴OA⊥OB.
(2)解:设直线与x轴交于N,又显然k≠0,
∴令y=0,则x=-1,即N(-1,0).
∵S△OAB=S△OAN+S△OBN
=![]() |ON||y1|+
|ON||y1|+![]() |ON||y2|
|ON||y2|
=![]() |ON|·|y1-y2|,
|ON|·|y1-y2|,
∴S△OAB=![]() ·1·
·1·![]() .
.
∵S△OAB=![]() ,∴
,∴![]() =
=![]() .
.
解之,得k=±![]() .
.

练习册系列答案
相关题目

 的焦点为F1.
的焦点为F1. ,又因为
,又因为 ,这样可知得到
,这样可知得到 。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到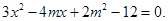 ,再利用
,再利用 可以结合韦达定理求解得到m的值和圆p的方程。
可以结合韦达定理求解得到m的值和圆p的方程。
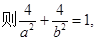 ①………………………………1分
①………………………………1分
 ………………………7分
………………………7分 、
、 ………………8分
………………8分
 ………………………9分
………………………9分 ……………………………10分
……………………………10分