题目内容
下列各命题中正确的命题是( )
①命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
②命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1≤3x”;
③“函数f(x)=cos2ax-sin2ax最小正周期为π”是“a=1”的必要不充分条件;
④“平面向量
与
的夹角是钝角”的充分必要条件是“
•
<0”.
①命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
②命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1≤3x”;
③“函数f(x)=cos2ax-sin2ax最小正周期为π”是“a=1”的必要不充分条件;
④“平面向量
| a |
| b |
| a |
| b |
| A.②③ | B.①②③ | C.①②④ | D.③④ |
①∵命题p或q中有一个为真命题,则命题“pVq”为真命题,∴①是假命题;
②根据“?x0∈R,p(x)”的否定是“?x∈R,¬p(x)”,可判断出:命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1≤3x”是真命题;
③∵若函数f(x)=cos2ax-sin2ax=cos2ax的最小正周期是π,则
=π,解得a=±1,故“函数f(x)=cos2ax-sin2ax最小正周期为π”是“a=1”的必要不充分条件是真命题;
④∵非零向量-
•
=-|
|2<0,但是-
与
的夹角是π,而不是钝角,故④是假命题.
综上可知只有②③是真命题.
故选A.
②根据“?x0∈R,p(x)”的否定是“?x∈R,¬p(x)”,可判断出:命题“?x0∈R,x02+1>3x0”的否定是“?x∈R,x2+1≤3x”是真命题;
③∵若函数f(x)=cos2ax-sin2ax=cos2ax的最小正周期是π,则
| 2π |
| |2a| |
④∵非零向量-
| a |
| a |
| a |
| a |
| a |
综上可知只有②③是真命题.
故选A.

练习册系列答案
相关题目
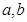 都是奇数,则
都是奇数,则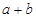 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若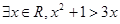 ”的否定是“
”的否定是“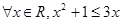 ” ;
” ;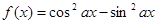 的最小正周期为
的最小正周期为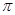 ” 是“
” 是“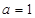 ”的必要不充分条件;
”的必要不充分条件;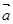 与
与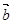 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“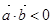 ” .
” . 都是奇数,则
都是奇数,则 是偶数”的逆否命题是“若
是偶数”的逆否命题是“若 ”的否定是“
”的否定是“ ”
;
”
; 的最小正周期为
的最小正周期为 ” 是“
” 是“ ”的必要不充分条件;
”的必要不充分条件; 与
与 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ”
.
”
. 都是奇数,则
都是奇数,则 是偶数”的逆否命题是“
是偶数”的逆否命题是“ ”的否定是“
”的否定是“ ”;
”; 的最小正周期为
的最小正周期为 ” 是“
” 是“ ”的必要不充分条件;
”的必要不充分条件; 与
与 的夹角是钝角”的充要条件是“
的夹角是钝角”的充要条件是“ ”.
”.
 ”的否定是“?x∈R,x2+1≤3x”;
”的否定是“?x∈R,x2+1≤3x”;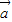 与
与 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ <0”.
<0”.