题目内容
已知圆的方程为 ,过点
,过点 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为 、
、 ,直线
,直线 恰好经过椭圆
恰好经过椭圆 的右顶点和上顶点.
的右顶点和上顶点.

(Ⅰ)求椭圆的方程;
(Ⅱ)设 是椭圆
是椭圆 (
( 垂直于
垂直于 轴的一条弦,
轴的一条弦, 所在直线的方程为
所在直线的方程为 且
且 是椭圆上异于
是椭圆上异于 、
、 的任意一点,直线
的任意一点,直线 、
、 分别交定直线
分别交定直线 于两点
于两点 、
、 ,求证
,求证 .
.
【答案】
(Ⅰ) (Ⅱ)联立方程组表示出向量
(Ⅱ)联立方程组表示出向量 ,再证.
,再证.
【解析】
试题分析:(Ⅰ)
观察知, 是圆的一条切线,切点为
是圆的一条切线,切点为 ,
,
设 为圆心,根据圆的切线性质,
为圆心,根据圆的切线性质, ,
,
所以 , 所以直线
, 所以直线 的方程为
的方程为 .
.
线 与
与 轴相交于
轴相交于 ,依题意
,依题意 ,所求椭圆的方程为
,所求椭圆的方程为
(Ⅱ)
椭圆方程为 ,设
,设


则有 ,
,
在直线 的方程
的方程 中,令
中,令 ,整理得
,整理得
 ①
①
同理, ②
②
① ②,并将
②,并将
 代入得
代入得


= =
= =
= .
.
而 =
=
∵ 且
且 ,∴
,∴
∴
考点:直线与圆锥曲线的关系;椭圆的标准方程.
点评:本题考查直线与圆锥曲线的位置关系,考查椭圆的标准方程,考查数形结合思想,考查学生的运算能力、分析问题解决问题的能力,难度较大.

练习册系列答案
相关题目
 的方程为
的方程为 ,直线
,直线 过点
过点 ,且与圆
,且与圆 轴交于
轴交于 两点,
两点, 是圆
是圆 且与
且与 ,直线
,直线 交直线
交直线 ,直线
,直线 交直线
交直线 .求证:
.求证: 的外接圆总过定点,并求出定点坐标.
的外接圆总过定点,并求出定点坐标. 的方程为
的方程为 ,过点
,过点 的直线
的直线 与圆
与圆 两点,若使
两点,若使 最小,则直线
最小,则直线 的方程为
的方程为 ,过点
,过点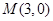 作直线与圆
作直线与圆 、
、 两点。
两点。
 ,求直线AB的方程;
,求直线AB的方程; 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率; 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。