题目内容
用数学归纳法证明: 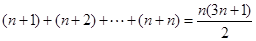
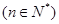 的第二步中,当
的第二步中,当 时等式左边与
时等式左边与 时的等式左边的差等于 .
时的等式左边的差等于 .
3k+2
解析试题分析:当 时等式左边为
时等式左边为 ,而
,而 时的等式左边为
时的等式左边为 ,所以差为
,所以差为
考点:数学归纳法

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
题目内容
用数学归纳法证明: 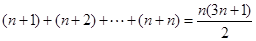
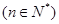 的第二步中,当
的第二步中,当 时等式左边与
时等式左边与 时的等式左边的差等于 .
时的等式左边的差等于 .
3k+2
解析试题分析:当 时等式左边为
时等式左边为 ,而
,而 时的等式左边为
时的等式左边为 ,所以差为
,所以差为
考点:数学归纳法

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案