题目内容
已知函数 在
在 处取得极值为
处取得极值为
(Ⅰ)求a、b的值;
(Ⅱ)若 有极大值28,求
有极大值28,求 在
在 上的最大值和最小值.
上的最大值和最小值.
解析】(Ⅰ)因 故
故 由于
由于 在点
在点 处取得极值
处取得极值
故有 即
即 ,
,
化简得 解得
解得 -
-
(Ⅱ)由(Ⅰ)知  ,
,
令 ,得
,得 当
当 时,
时,
 故
故 在
在 上为增函数;
上为增函数;
当 时,
时, 故
故 在
在 上为减函数
上为减函数
当 时
时 ,故
,故 在
在 上为增函数。
上为增函数。
由此可知 在
在 处取得极大值
处取得极大值 ,
, 在
在 处取得极小值
处取得极小值 由题设条件知
由题设条件知 得
得
此时 ,
,
因此 上
上 的最小值为
的最小值为 ,最大值为f(-2)=28。
,最大值为f(-2)=28。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
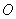 为
为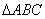 的外心,
的外心,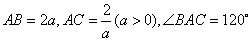 ,若
,若 (
( ,
, 为实数),则
为实数),则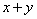 的最小值为 .
的最小值为 . 中,
中, ,
, ,试猜想出这个数列的通项公式为
,试猜想出这个数列的通项公式为 大值也无极小值 D.既有极大值又有极小值
大值也无极小值 D.既有极大值又有极小值 ___________.
___________. ,那么在程序UNTIL后面的“条件”应为( )
,那么在程序UNTIL后面的“条件”应为( )
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( ) 

 C
C

 ,直线
,直线 与圆
与圆 相切,且交椭圆
相切,且交椭圆 于
于 两点,c是椭圆的半焦距,
两点,c是椭圆的半焦距, .
. ,求椭圆
,求椭圆 的方程;
的方程; ,直线
,直线 与直线
与直线 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.