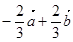题目内容
已知AD,BE分别是△ABC的边BC,AC上的中线,且
=
,
=
,则
=
-
-
.
| AD |
| a |
| BE |
| b |
| AB |
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
分析:设G为AD、BE的交点,则G是△ABC的重心,故有
=
=
,且
=-
=-
;故有
=
+
,化简得到结果.
| AG |
| 2 |
| 3 |
| AD |
| 2 |
| 3 |
| a |
| GB |
| 2 |
| 3 |
| BE |
| 2 |
| 3 |
| b |
| AB |
| AG |
| GB |
解答:解:设G为AD、BE的交点,∵AD,BE分别是△ABC的边BC,AC上的中线,
∴G是△ABC的重心,
∴
=
=
,且
=-
=-
.
故
=
+
=
-
.
故答案为
-
.
∴G是△ABC的重心,
∴
| AG |
| 2 |
| 3 |
| AD |
| 2 |
| 3 |
| a |
| GB |
| 2 |
| 3 |
| BE |
| 2 |
| 3 |
| b |
故
| AB |
| AG |
| GB |
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
故答案为
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
点评:本题主要考查平面向量基本定理及其几何意义,三角形的重心的性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
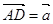 ,
, ,则
,则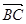 =( )
=( )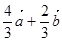 B.
B.  C.
C.
 D.
D.