题目内容
在下列四个函数中,在[1,+∞)是减函数的是
- A.y=x2-2x-1
- B.

- C.y=2|x|
- D.

B
分析:利用二次函数的性质可得A不满足条件,利用函数的单调性的定义证明函数 在[1,+∞)是减函数,利用指数函数性质可得y=2|x| 在[1,+∞)是增函数,故C不满足条件,利用对数函数的性质可得函数y=
在[1,+∞)是减函数,利用指数函数性质可得y=2|x| 在[1,+∞)是增函数,故C不满足条件,利用对数函数的性质可得函数y= 在[1,+∞)是增函数,故排除D,从而得出结论.
在[1,+∞)是增函数,故排除D,从而得出结论.
解答:由二次函数y=x2-2x-1的对称轴为x=1可得,二次函数y=x2-2x-1在[1,+∞)是增函数,故排除B.
设函数 =f(x),设x2>x1≥1,由于f(x2)-f(x1)=
=f(x),设x2>x1≥1,由于f(x2)-f(x1)=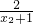 -
-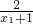 =
= <0,故f(x2)<f(x1),
<0,故f(x2)<f(x1),
故函数 =f(x) 在[1,+∞)是减函数,故B满足条件.
=f(x) 在[1,+∞)是减函数,故B满足条件.
当 x∈[1,+∞)时,函数y=2|x| 即y=2x,显然函数y=2|x| 在[1,+∞)是增函数,故排除C.
当 x∈[1,+∞)时,函数y= =-
=- =
= =lgx,显然此函数在[1,+∞)是增函数,故排除D.
=lgx,显然此函数在[1,+∞)是增函数,故排除D.
故选B.
点评:本题主要考查函数的单调性的判断和证明,属于基础题.
分析:利用二次函数的性质可得A不满足条件,利用函数的单调性的定义证明函数
 在[1,+∞)是减函数,利用指数函数性质可得y=2|x| 在[1,+∞)是增函数,故C不满足条件,利用对数函数的性质可得函数y=
在[1,+∞)是减函数,利用指数函数性质可得y=2|x| 在[1,+∞)是增函数,故C不满足条件,利用对数函数的性质可得函数y= 在[1,+∞)是增函数,故排除D,从而得出结论.
在[1,+∞)是增函数,故排除D,从而得出结论.解答:由二次函数y=x2-2x-1的对称轴为x=1可得,二次函数y=x2-2x-1在[1,+∞)是增函数,故排除B.
设函数
 =f(x),设x2>x1≥1,由于f(x2)-f(x1)=
=f(x),设x2>x1≥1,由于f(x2)-f(x1)=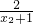 -
-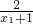 =
= <0,故f(x2)<f(x1),
<0,故f(x2)<f(x1),故函数
 =f(x) 在[1,+∞)是减函数,故B满足条件.
=f(x) 在[1,+∞)是减函数,故B满足条件.当 x∈[1,+∞)时,函数y=2|x| 即y=2x,显然函数y=2|x| 在[1,+∞)是增函数,故排除C.
当 x∈[1,+∞)时,函数y=
 =-
=- =
= =lgx,显然此函数在[1,+∞)是增函数,故排除D.
=lgx,显然此函数在[1,+∞)是增函数,故排除D.故选B.
点评:本题主要考查函数的单调性的判断和证明,属于基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
在下列四个函数中,在区间(0,
)上为增函数,且以π为最小正周期的偶函数是( )
| π |
| 2 |
| A、y=tanx |
| B、y=sin|x| |
| C、y=cos2x |
| D、y=|sinx| |
 上为增函数,且以
上为增函数,且以 为最小正周期的偶函数是( )
为最小正周期的偶函数是( ) )上为增函数,且以π为最小正周期的偶函数是( )
)上为增函数,且以π为最小正周期的偶函数是( ) )上为增函数,且以π为最小正周期的偶函数是( )
)上为增函数,且以π为最小正周期的偶函数是( )