题目内容
把函数 的图象向右平移φ(φ>0)个单位后图象关于y轴对称,则φ的最小值为
的图象向右平移φ(φ>0)个单位后图象关于y轴对称,则φ的最小值为
- A.

- B.

- C.

- D.

A
分析:函数的解析式即 y= ,把它的图象向右平移φ个单位所得图象对应的函数解析式为y=
,把它的图象向右平移φ个单位所得图象对应的函数解析式为y= .要使此函数为偶函数,正实数φ的最小值满足-2φ+
.要使此函数为偶函数,正实数φ的最小值满足-2φ+ =π,由此求得φ的最小值.
=π,由此求得φ的最小值.
解答:函数 =
= .
.
把函数y= 的图象向右平移φ个单位,
的图象向右平移φ个单位,
所得图象对应的函数解析式为y= .
.
由题意可得y=cos(2x-2φ+ ) 是偶函数,故正实数φ的最小值满足-2φ+
) 是偶函数,故正实数φ的最小值满足-2φ+ =π,
=π,
故正实数φ的最小值为 ,
,
故选A.
点评:本题主要考查三角函数的对称性,函数y=Acos(ωx+∅)的图象变换,属于中档题.
分析:函数的解析式即 y=
 ,把它的图象向右平移φ个单位所得图象对应的函数解析式为y=
,把它的图象向右平移φ个单位所得图象对应的函数解析式为y= .要使此函数为偶函数,正实数φ的最小值满足-2φ+
.要使此函数为偶函数,正实数φ的最小值满足-2φ+ =π,由此求得φ的最小值.
=π,由此求得φ的最小值.解答:函数
 =
= .
.把函数y=
 的图象向右平移φ个单位,
的图象向右平移φ个单位,所得图象对应的函数解析式为y=
 .
.由题意可得y=cos(2x-2φ+
 ) 是偶函数,故正实数φ的最小值满足-2φ+
) 是偶函数,故正实数φ的最小值满足-2φ+ =π,
=π,故正实数φ的最小值为
 ,
,故选A.
点评:本题主要考查三角函数的对称性,函数y=Acos(ωx+∅)的图象变换,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
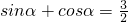 ;
;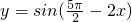 是偶函数;
是偶函数; 是函数
是函数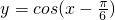 图象的一条对称轴方程;
图象的一条对称轴方程;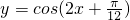 的图象向右平移
的图象向右平移 个单位,所得的函数解析式为
个单位,所得的函数解析式为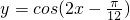
 的图象关于点
的图象关于点 对称;
对称; 的最小正周期是π;
的最小正周期是π; 的图象向右平移
的图象向右平移 个单位可得到y=2sin2x的图象.
个单位可得到y=2sin2x的图象.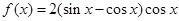 的四个结论:
的四个结论: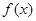 的最大值为
的最大值为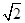 ;
;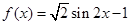 的图象向右平移
的图象向右平移 个单位后可得到函数
个单位后可得到函数 ],
],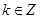 ;
; 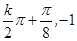 ),
),