题目内容
已知数列{an}的首项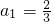 ,
, ,n∈N+
,n∈N+
(Ⅰ)设 证明:数列{bn}是等比数列;
证明:数列{bn}是等比数列;
(Ⅱ)数列{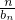 }的前n项和Sn.
}的前n项和Sn.
解:(Ⅰ)∵数列{an}的首项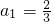 ,
, ,
,
∴a2= =
= ,
,
a3= =
= ,
,
a4= =
=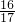 .
.
由此猜想an= .
.
用数学归纳法证明:
①当n-1时, =
= ,成立;
,成立;
②假设n=k时,等式成立,即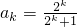 ,
,
则 =
= =
=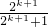 ,成立.
,成立.
∴an= .
.
∴ =
= -1=
-1= .
.
∵b1= -1=
-1= -1=
-1= ,
, =
= =
= ,
,
∴数列{bn}是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
(Ⅱ)∵bn= ,
,
∴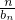 =n•2n,
=n•2n,
∴数列{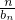 }的前n项和
}的前n项和
Sn=1×2+2×22+3×23+…+n×2n,①
∴2Sn=1×22+2×23+3×24+…+n×2n+1,②
①-②,得-Sn=2+22+23+24+…+2n-n×2n+1
= -n×2n+1
-n×2n+1
=-(2-2n+1+n×2n+1),
∴Sn=2-2n+1+n×2n+1=(n-1)•2n+1+2.
分析:(Ⅰ)由数列{an}的首项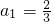 ,
, ,推导出an=
,推导出an= .所以
.所以 =
= .由此能够证明数列{bn}是等比数列.
.由此能够证明数列{bn}是等比数列.
(Ⅱ)由bn= ,知
,知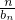 =n•2n,故数列{
=n•2n,故数列{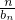 }的前n项和Sn=1×2+2×22+3×23+…+n×2n,由此利用错位相减法能求出数列{
}的前n项和Sn=1×2+2×22+3×23+…+n×2n,由此利用错位相减法能求出数列{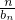 }的前n项和Sn.
}的前n项和Sn.
点评:本题考查等比数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意数学归纳法、错位相减法和递推思想的合理运用.
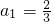 ,
, ,
,∴a2=
 =
= ,
,a3=
 =
= ,
,a4=
 =
=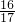 .
.由此猜想an=
 .
.用数学归纳法证明:
①当n-1时,
 =
= ,成立;
,成立;②假设n=k时,等式成立,即
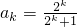 ,
,则
 =
= =
=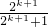 ,成立.
,成立.∴an=
 .
.∴
 =
= -1=
-1= .
.∵b1=
 -1=
-1= -1=
-1= ,
, =
= =
= ,
,∴数列{bn}是首项为
 ,公比为
,公比为 的等比数列.
的等比数列.(Ⅱ)∵bn=
 ,
,∴
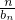 =n•2n,
=n•2n,∴数列{
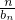 }的前n项和
}的前n项和Sn=1×2+2×22+3×23+…+n×2n,①
∴2Sn=1×22+2×23+3×24+…+n×2n+1,②
①-②,得-Sn=2+22+23+24+…+2n-n×2n+1
=
 -n×2n+1
-n×2n+1=-(2-2n+1+n×2n+1),
∴Sn=2-2n+1+n×2n+1=(n-1)•2n+1+2.
分析:(Ⅰ)由数列{an}的首项
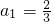 ,
, ,推导出an=
,推导出an= .所以
.所以 =
= .由此能够证明数列{bn}是等比数列.
.由此能够证明数列{bn}是等比数列.(Ⅱ)由bn=
 ,知
,知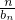 =n•2n,故数列{
=n•2n,故数列{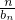 }的前n项和Sn=1×2+2×22+3×23+…+n×2n,由此利用错位相减法能求出数列{
}的前n项和Sn=1×2+2×22+3×23+…+n×2n,由此利用错位相减法能求出数列{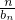 }的前n项和Sn.
}的前n项和Sn.点评:本题考查等比数列的证明,考查数列的前n项和的求法,解题时要认真审题,注意数学归纳法、错位相减法和递推思想的合理运用.

练习册系列答案
相关题目