题目内容
已知对任意的x>0恒有a1nx≤b(x-1)成立.
(1)求正数a与b的关系;
(2)若a=1,设f(x)=m
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
(3)证明:1n(n!)>2n-4
(n∈N,n≥2)
(1)求正数a与b的关系;
(2)若a=1,设f(x)=m
| x |
(3)证明:1n(n!)>2n-4
| n |
(1)设f(x)=alnx-b(x-1),
易知f(1)=0,由已知f(x)≤0恒成立,
所以函数f(x)在x=1处取得最大值.f′(x)=
-b=
∴f'(1)=0,∴a=b
又∵a>0,∴f(x)在x=1处取得极大值,符合题意,
即关系式为a=b.(3分)
(2)∵a=1,∴b=1∴lnx≤m
+n≤x-1恒成立,
令x=1,有0≤m+n≤0,∴m+n=0(5分)∴m
+m≤x-1,
即(
-1)(
+1-m)≥0对?x>0恒成立,∴须1-m=-1,即m=2∴函数f(x)=2(
-1)(7分)
(3)由(2)知:ln
≤
-2=
-2<
-2=4(
-
)-2(9分)
∴ln
<4[(
-
)+(
-
)++(
-
)]-2n=4
-2n
即lnn!>2n-4
(n∈N,n≥2)(12分)
易知f(1)=0,由已知f(x)≤0恒成立,
所以函数f(x)在x=1处取得最大值.f′(x)=
| a |
| x |
| a-bx |
| x |
又∵a>0,∴f(x)在x=1处取得极大值,符合题意,
即关系式为a=b.(3分)
(2)∵a=1,∴b=1∴lnx≤m
| x |
令x=1,有0≤m+n≤0,∴m+n=0(5分)∴m
| x |
即(
| x |
| x |
| x |
(3)由(2)知:ln
| 1 |
| k |
| 2 | ||
|
| 4 | ||
2
|
| 4 | ||||
|
| k |
| k-1 |
∴ln
| 1 |
| n! |
| n |
| n-1 |
| n-1 |
| n-2 |
| 1 |
| 0 |
| n |
即lnn!>2n-4
| n |

练习册系列答案
相关题目
 +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式; (n∈N,n≥2)
(n∈N,n≥2)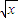 +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;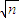 (n∈N,n≥2)
(n∈N,n≥2) +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式; (n∈N,n≥2)
(n∈N,n≥2) +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式; (n∈N,n≥2)
(n∈N,n≥2)