题目内容
已知对任意的x>0恒有a1nx≤b(x-1)成立.(1)求正数a与b的关系;
(2)若a=1,设f(x)=m
 +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;(3)证明:1n(n!)>2n-4
 (n∈N,n≥2)
(n∈N,n≥2)
【答案】分析:(1)由条件构造函数,进而把不等式问题转化为函数的最值问题,求导,从而得到a与b的关系;
(2)待定系数法求函数的解析式,注意不等式中等号成立的条件,是解答此题的关键;
(3)借助于(2)的结论来证明(3),利用放缩法达到证明不等式的目的.
解答:解:(1)设f(x)=alnx-b(x-1),
易知f(1)=0,由已知f(x)≤0恒成立,
所以函数f(x)在x=1处取得最大值. ∴f'(1)=0,∴a=b
∴f'(1)=0,∴a=b
又∵a>0,∴f(x)在x=1处取得极大值,符合题意,
即关系式为a=b.(3分)
(2)∵a=1,∴b=1∴ 恒成立,
恒成立,
令x=1,有0≤m+n≤0,∴m+n=0(5分)∴ ,
,
即 对?x>0恒成立,∴须1-m=-1,即m=2∴函数
对?x>0恒成立,∴须1-m=-1,即m=2∴函数 (7分)
(7分)
(3)由(2)知: (9分)
(9分)
∴ =
=
即 (12分)
(12分)
点评:利用函数的单调性、最值证明不等式,体现了导数的作用;不等式等号成立的条件,体现了赋值法求某点的函数值.
(2)待定系数法求函数的解析式,注意不等式中等号成立的条件,是解答此题的关键;
(3)借助于(2)的结论来证明(3),利用放缩法达到证明不等式的目的.
解答:解:(1)设f(x)=alnx-b(x-1),
易知f(1)=0,由已知f(x)≤0恒成立,
所以函数f(x)在x=1处取得最大值.
 ∴f'(1)=0,∴a=b
∴f'(1)=0,∴a=b又∵a>0,∴f(x)在x=1处取得极大值,符合题意,
即关系式为a=b.(3分)
(2)∵a=1,∴b=1∴
 恒成立,
恒成立,令x=1,有0≤m+n≤0,∴m+n=0(5分)∴
 ,
,即
 对?x>0恒成立,∴须1-m=-1,即m=2∴函数
对?x>0恒成立,∴须1-m=-1,即m=2∴函数 (7分)
(7分)(3)由(2)知:
 (9分)
(9分)∴
 =
=
即
 (12分)
(12分)点评:利用函数的单调性、最值证明不等式,体现了导数的作用;不等式等号成立的条件,体现了赋值法求某点的函数值.

练习册系列答案
相关题目
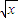 +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;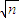 (n∈N,n≥2)
(n∈N,n≥2) +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式; (n∈N,n≥2)
(n∈N,n≥2) +n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式;
+n,(m,n∈R),若1nx≤f(x)≤b(x-1)对?x>0恒成立,求函数f(x)的解析式; (n∈N,n≥2)
(n∈N,n≥2)