题目内容
【题目】设函数f(x)=sinxcosx将 f(x)的图象向右平移 ![]() (0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=
(0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x= ![]() .
.
(1)求φ;
(2)求函数y=g(x)的单调增区间.
【答案】
(1)解:f(x)= ![]() sin2x,g(x)=
sin2x,g(x)= ![]() sin(2x﹣φ)
sin(2x﹣φ)
∵x= ![]() 是函数y=g(x)图象的对称轴.
是函数y=g(x)图象的对称轴.
∴sin(2× ![]() ﹣φ)=±1,
﹣φ)=±1, ![]() ﹣φ=kπ+
﹣φ=kπ+ ![]() ,k∈Z.
,k∈Z.
∵0<φ<π,∴φ= ![]()
(2)解:由(1)知φ= ![]() ,因此y=sin(2x﹣
,因此y=sin(2x﹣ ![]() ).
).
由题意得2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z.
,k∈Z.
∴函数y=sin(2x﹣ ![]() )的单调增区间为[kπ+
)的单调增区间为[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
【解析】(1)由已知利用平移变换规律可求g(x)= ![]() sin(2x﹣φ),由sin(2×
sin(2x﹣φ),由sin(2× ![]() ﹣φ)=±1,可求
﹣φ)=±1,可求 ![]() ﹣φ=kπ+
﹣φ=kπ+ ![]() ,k∈Z,结合范围0<φ<π,即可得解φ的值.(2)由2kπ﹣
,k∈Z,结合范围0<φ<π,即可得解φ的值.(2)由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可解得函数y=sin(2x﹣
,k∈Z,即可解得函数y=sin(2x﹣ ![]() )的单调增区间.
)的单调增区间.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

 优翼小帮手同步口算系列答案
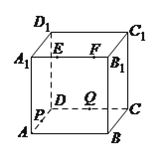
优翼小帮手同步口算系列答案【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,动点
,动点![]() 、
、![]() 在棱
在棱![]() 上,动点
上,动点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上,若
上,若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 大于零),则四面体
大于零),则四面体![]() 的体积( ).
的体积( ).
A. 与![]() ,
,![]() ,
,![]() 都有关 B. 与
都有关 B. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
C. 与![]() 有关,与
有关,与![]() ,
,![]() 无关 D. 与
无关 D. 与![]() 有关,与
有关,与![]() ,
,![]() 无关
无关
【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于![]() 为合格品,小于
为合格品,小于![]() 为次品.现随机抽取这种芯片共
为次品.现随机抽取这种芯片共![]() 件进行检测,检测结果统计如表:
件进行检测,检测结果统计如表:
测试指标 |
|
|
|
|
|
芯片数量(件) |
|
|
|
|
|
已知生产一件芯片,若是合格品可盈利![]() 元,若是次品则亏损
元,若是次品则亏损![]() 元.
元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产![]() 件芯片所获得的利润不少于
件芯片所获得的利润不少于![]() 元的概率.
元的概率.
(Ⅱ)记![]() 为生产
为生产![]() 件芯片所得的总利润,求随机变量
件芯片所得的总利润,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
