题目内容
设函数 (
(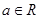 ),其导函数为
),其导函数为 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)当 时,
时, ,求证:
,求证: .
.
(1)单调增区间为 ,单调减区间为
,单调减区间为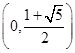 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)求单调区间是常规问题,但需注意定义域先行,步骤是:①先求定义域;②后求导数 ;③令
;③令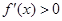 结合定义域得增区间,令
结合定义域得增区间,令 结合定义域得减区间,最后结果一定要用区间表示;(2)掌握好执因索果,即分析法在此题中的应用,以及与基本不等式的结合.
结合定义域得减区间,最后结果一定要用区间表示;(2)掌握好执因索果,即分析法在此题中的应用,以及与基本不等式的结合.
试题解析:(1)当 时,
时,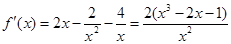 (
( )
)
令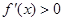 ,即:
,即: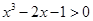 ,
,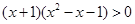
解得: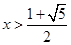 ,所以:函数
,所以:函数 的单调增区间为
的单调增区间为 ,
,
同理:单调减区间为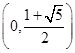 .
.
(2)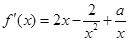 ,所以:
,所以:


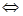
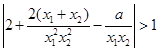 ,
,
下面证明 ,有
,有 恒成立,
恒成立,
即证: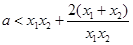 成立,
成立,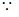
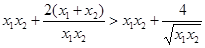 ,
,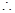 只需证明:
只需证明: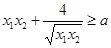 即可,
即可,
对此:设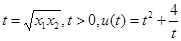 ,
,
而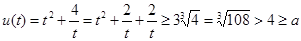
所以: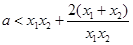 .故命题得证.
.故命题得证.
考点:1.导数的应用;2.不等式的证明方法;3.创设条件使用基本不等式.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
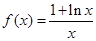 .
. 在区间
在区间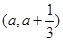
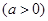 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围; 时,不等式
时,不等式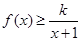 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围; 。
。 处的切线方程;
处的切线方程; 对任意的
对任意的 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。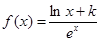 (k为常数,e=2.71828…是自然对数的底数),曲线
(k为常数,e=2.71828…是自然对数的底数),曲线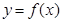 在点
在点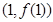 处的切线与x轴平行.
处的切线与x轴平行.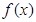 的单调区间;
的单调区间; 其中
其中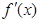 为
为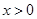 ,
,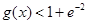 .
. 在
在 与
与 处都取得极值.
处都取得极值. 的解析式;
的解析式;
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数). 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值.
 .
. 时,求函数
时,求函数 的极大值;
的极大值; 的图象有三个不同的交点,求
的图象有三个不同的交点,求 的取值范围;
的取值范围; ,当
,当 时,求函数
时,求函数 的单调减区间.
的单调减区间. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 时
时 ,求a的取值范围.
,求a的取值范围.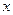 件的总成本
件的总成本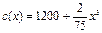 (万元),又知产品单价的平方与产品件数
(万元),又知产品单价的平方与产品件数